Ich habe jetzt einige Ansätze gemacht und auch eine Lösung, bei der ich mir nicht ganz sicher bin.
Ich habe dazu die unten verzeichnete Zeichnung verwendet.
Als die Pyramide habe ich die Seitenflächenhöhen verwendet, in denen der Quader diese Position haben muss.
Ich habe folgenede Größen benutzt: L = 5*sqrt(3) / 2 , a= 5* sqrt(2) / 2
Als Volumenformel ergab sich folgendes:
V(x) = 4* (0,25 * x)^2 * ( 5√2 / 2 - x)
= x^2 * (5√2 / 2 -x)
V(x) = -x^3 + 5√2 / 2 *x^2
Davon bildete ich dann die 1. und 2. Ableitung und setzte den passenden x-Wert in die Volumenformel ein.
Als maximales Volumen bekam ich 6, 547285011 VE heraus.
Auf den Oktaeder gerechnet beträgt das max. Volumen 6, 547285011 * 2 VE.
Wäre das richtig oder habe ich etwas übersehen?
Würde mich sehr freuen, wenn sie mir ggf. Tipps oder Verbesserungen geben würden.
Ich habe mich an dieser Seite orientiert: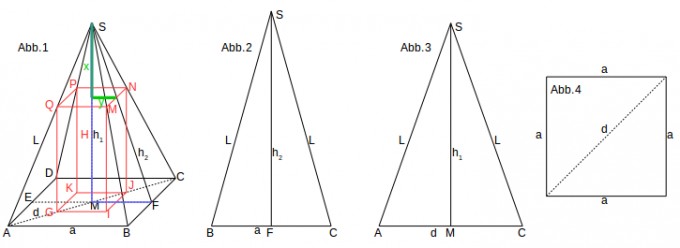
http://gfs.khmeyberg.de/1415/1415Klasse10eMa/1415UnterrichtMathematik10eFunktionsuntersuchungen.html