Wie löst man diese Mengenaufgaben?

Question

Sei

Welche Mengen werden durch

a)     b) 

Wie soll dies funktionieren?

Answer 1

Du betrachtest hier eine Folge von Intervallen, beginnend bei k=1. Das sieht dann so aus:

$$ I_1=\Bigg[-1,2+\frac{1}{1} \Bigg] $$

k=2

$$ I_2=\Bigg[-2,2+\frac{1}{2} \Bigg] $$

Und das geht halt immer so weiter. Nun sollst du einmal all diese Mengen vereinigen und einmal schneiden und gucken, was dabei als Endresultat entsteht.

Vereinigungsmenge alle I_k

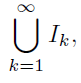
Schnittmenge aller I_k

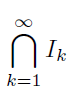
Weil das hier alles Intervalle sind, kannst du dir mal eine Skizze in Form eines Zahlenstrahles zu jedem Fall machen, damit du dir schonmal anschaulich vorstellen kannst, was passiert, wenn du alle Intervalle vereinigst, bzw. schneidest.

Comments

Also Wäre a) ]-infty,2[U]2,3]?

Und wenn ich alle schneide, müsste da nicht Null rauskommen? BTW die leere Menge?

Ich kann mir das leider nicht so gut vorstellen.

---

a) Wäre so.

$$ \bigcup_{k=1}^\infty I_k=]-\infty,3]=\mathbb{R^-}\cup[0,3] $$

Stell es dir bei der Vereinigung einfach so vor. Du legst alle Intervalle übereinander. Dann ,,sieht'' man was man für ein Gesamtintervall bekommt. Hier mal eine Bildfolge der Intervalle für k=1, k=2, k=3, k=4 und k=10, usw. Bei der Schnittmenge schaust du anders. Du stellst dir dann die Frage: Was haben alle Mengen denn gemeinsam, bzw. was haben denn alle diese Mengen, also die Intervalle?

---

Achso, danke dir für die Erklärung

Dann wäre b) :

[-1,2]? Das ja 1/k für k->infty = 0 ist.

---

Genau. Es bleibt am Ende nur noch dieser ,,Streifen", also [-1,2] übrig.