Sei G⊂ R n ein konvexes Gebiet, f: G → Rn stetig differenzierbar und es gelte
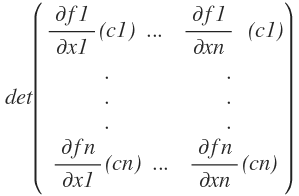
Dann ist f Injektiv.
a) Beweisen Sie dieses Kriterium für globale Umkehrbarkeit mit Hilfe des Mittelwertsatzes der Differentialrechnung
im R n .
b) Sei G=(0,∞) und f: G → R2 definiert durch
f(x) = 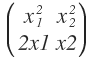
Ist f Injektiv? Wenden Sie das Kriterium an.