lösungsmenge einer faktorisierten form von gr. funktion bestimmen

Question

(thema ganzrationale funktionen) die aufgabe lautet:

Bestimme die Lösungen von:
12 · ( x− 4) · (x + 5)²  = 0

da die funktionsgleichung gleich null gesetzt wurde, gehe ich davon aus dass die nullstellen gesucht sind aber sind die nicht schon eig gegeben? x_{1 =}  4 und x₂ = -5

aber egal ich hab es ausgeklammert und am ende steht bei mir: 12x³ + 6x² - 15x -100 soll ich jetzt die polynomdivision anwenden oder war mit der aufgabenstellung gemeint ich soll die nullstellen einfach ablesen durch die faktorisierte form?

Answer 1

Genau. -5 ist sogar eine doppelte Nullstelle (wegen Quadrat), bei der f die x-Achse nur berührt und nicht schneidet. Polynomdivision ist hier unnötig, da du f schon als Produkt hast und sogar gleich Null ist. Satz vom Nullprodukt gibt dir schnell die Nullstellen: Ein Produkt ist Null, wenn einer der Faktoren gleich Null ist.

Comments

Da ich herausbekommen habe, dass es eine Polynomfunktion dritten Grades ist, hat sie also maximal 3 Nullstellen, ablesen können wir 2. Soll man sich dann normalerweise auf der Suche nach einer dritten Nullstelle begeben bzw. woran erkennt man, dass es nicht die maximale Anzahl an Nullstellen gibt?

---

Wie oft welche Nullstelle vorkommt sieht man bei der faktorisierten Form eines Polynoms, also wenn er in Linearfaktoren vorliegt. Nun kann es wie in deinem Beispiel auch vorkommen, dass dein Polynom nicht nur in unterschiedliche Linearfaktoren zerfällt, sondern, dass Linearfaktoren mehrmals vorkommen, bei dir (x+5).

Führt man eine Polynomdivision durch, dann muss ja die erste Nullstelle geraten werden. Dann macht man die Division und erhält ein neues Polynom, dessen Grad um eins verringert ist. Dann führt man nochmal durch Raten eine Polynomdivision durch. Da kann es passieren, dass man wieder dieselbe Nullstelle wie davor hatte. Der Linearfaktor kommt mehr als einmal vor.

Hier ein Beispiel:

f(x)=(x+2)(x+3)(x+3)(x-2)

Ausmultipliziert ergibt das:

f)x)=x^4+6x^3+5x^2-24x-36

Bei der Polynomdivision wirst du dann merken, dass x=-3 doppelt vorkommen wird.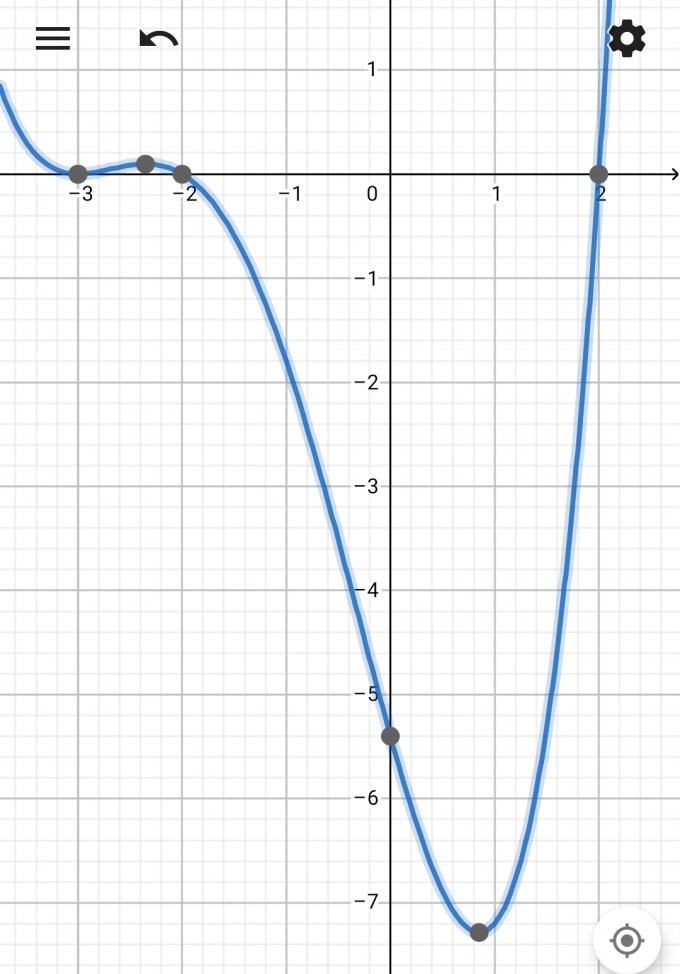

Bei x=-3 berührt f die x-Achse nur.

Im Endeffekt ist natürlich nicht wirklich bedeutend mehr sinnvoll zu sagen,,f hat Nullstellen bei x=-3, x=-3, x=2 und x=-2. Sondern man nimmt dann von jeden der Nullstellen nur eine für die Lösungsmenge, denn -3=-3.