Hallo mistermathe,
für a) und b) sollte es doch kein Problem sein. Bilde zunächst eine Geradengleichung in Parameterform. Im Falle von a):
$$f(t) = \begin{pmatrix} x(t)\\ y(t)\end{pmatrix} = P + t \cdot (Q - P) = \begin{pmatrix}-3\\ 2\end{pmatrix} + t \cdot \begin{pmatrix}18\\ 27\end{pmatrix} $$ und da nur die Strecke \(PQ\) abgebildet werden soll, ist der Definitionsbereich
$$t \in [0 \dots 1]$$ die Funktionen sind dann $$x(t) = -3 + 18t \text{;} \quad y(t) = 2 + 27t$$ bei b) geht es genauso: $$f(t) = R + t \cdot (S-R)= \begin{pmatrix}8\\ 8\end{pmatrix} + t \cdot \begin{pmatrix}-10\\ 30\end{pmatrix}$$ mit den Funktionen: $$x(t) = 8 -10t\text{;} \quad y(t) = 8 + 30 t$$ mit dem Unterschied, dass hier die ganze Gerade abgebildet werden soll - also \(t \in \mathbb{R}\)
Bei c) gibt es - wie schon erwähnt - unendlich viele Möglichkeiten. Ich stelle Dir hier eine vor, die Du in der Schule nicht lernst. Den Definitionsbereich legen wir im Vorfeld bereits mit \(t \in [0 \dots 1]\) fest. Bei \(t=0\) soll sich \(f(t)\) im Punkt \(A\), bei \(t=0,5\) bei \(B\) und bei \(t=1\) in \(C\) befinden. Dazu brauchen wir drei linearen Funktionen, deren Nullstellen jeweils bei \(0\), \(0,5\) und \(1\) liegen:
$$\begin{aligned} h_0 &= t \\ h_{0,5} &= 2t-1 \\ h_1 &= t-1 \end{aligned}$$ Jetzt bilden wir drei weitere Funktionen, die in allen Punkten, die nicht den aktuellen Punkt betreffen, zu 0 werden (ich erklär's gleich näher).
$$\begin{aligned} w_A(t) &= h_{0,5} \cdot h_{1} &&= (2t-1)(t-1)\\ w_B(t) &= -4 \cdot h_0 \cdot h_1 &&= 4t(1-t)\\ w_C(t) &= h_0 \cdot h_{0,5} &&= t(2t-1)\end{aligned}$$ Die Faktoren (hier die \(-4\)) dienen nur dazu, die Funktion auf 1 zu normieren; \(w_B(0,5)\) muss =1 sein. Jetzt setze ich alles zu \(f(t)\) zusammen:
$$f(t) = w_A \cdot A + w_B \cdot B + w_C \cdot C$$ was habe ich jetzt erreicht? Nun - wenn \(t=0\) ist, dann sind \(w_B\) und \(w_C\) ebenso gleich 0 - also ist \(f(0)=A\). Ist \(t=0,5\), dann sind \(w_A\) und \(w_C\) gleich 0 - also ist \(f(0,5)=B\) und genauso ist \(f(1)=C\). Im Bild sieht das so aus:
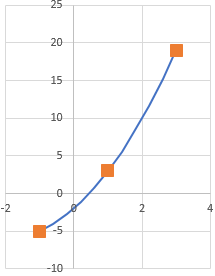
Das Ausmultiplizieren von \(f(t)\) zu den Funktionen \(x(t)\) und \(y(t)\) überlasse ich Dir ;-)
Der Vorteil dieser Vorgehensweise ist, dass es dabei völlig egal ist, wie die drei Punkte A, B und C liegen. Sie dürfen auch auf einander liegen. Weiterhin ist das Ergebnis unabhängig vom gewählten Koordinatensystem - die Kurve ist imme die gleiche. Wenn Du eine Parabel durch die Punkte legen würdest, also eine Funktion der Art \(f(x)=ax^2+bx+c\) geht das in diesem speziellen Fall auch, im allgemeinen Fall aber nicht und es ist weniger elegant.