Begründen Sie, dass (u x v)*(x-p)=0 eine Gleichung der Ebene mit dem Stützvektor p und den Spannvektoren u und v

Question

Begründen Sie, dass \( (\vec{u} \times \vec{v}) \cdot(\vec{x}-\vec{p})=0 \) eine Gleichung der Ebene mit dem Stützvektor \( \vec{p} \) und den Spannvektoren \( \vec{u} \) und \( \vec{v} \) beschreibt.

Stellen Sie die Ebene E: \( \left(\left(\begin{array}{l}2 \\ 0 \\ 3\end{array}\right) \times\left(\begin{array}{c}3 \\ -5 \\ 2\end{array}\right)\right) \cdot\left(\vec{x}-\left(\begin{array}{c}4 \\ -1 \\ 0\end{array}\right)\right)=0 \) im Koordinatensystem dar.

Answer 1

Wir wissen das u × v senkrecht zu u und zu v ist. Damit ist (u × v) Also senkrecht zur Ebene E.
Das bedeutet das alle Vektoren die durch 2 beliebige Punkte der Ebene gehen senkrecht zu (u × v) sind.

Wenn das Skalarprodukt zweier Vektoren null ist bilden die Vektoren einen rechten Winkel.
Da (u × v) * (x - p) = 0 ist ist der Vektor PX senkrecht zu (u × v). Wenn jetzt P in der Ebene liegt muss auch X in der Ebene liegen. Wenn alle X in der Ebene liegen ist das also eine Gleichung der Ebene.

Hier eine Skizze zu deiner Aufgabe

Comments

Vielen Dank :) Dennoch könntest du Vielleicht das ab "Wenn jetzt p in der Ebene......" nochmal erklären, aber wenn möglich ein bisschen ausführlicher oder in anderen Worten :) @Der_Mathecoach

---

Ich wiederhole das davor noch mal

Das bedeutet das alle Vektoren die durch 2 beliebige Punkte der Ebene gehen senkrecht zu (u × v) sind. 

Wenn also nur ein Punkt in der ebene liegt und der andere nicht in der Ebene, dann wäre der Vektor zwischen den Punkten nicht mehr senkrecht.

Mach mal ein Experiment wenn du am Tisch sitzt. Stell dir vor der Tisch ist eine Ebene. Ist denke ich nicht schwer vorstellbar. Und jetzt nimmst du einen Stift, der senkrecht von der Tischplatte wegzeigt. Das ist jetzt dein Normalenvektor u * v.

Der Punkt des Tisches unter dem Stift (wir nennen ihn mal P) ist ein Punkt in der Tisch-Ebene. Jetzt nimmst du andere Punkte im Raum (du nennst sie X) und fragst dich für Welche Punkte X der Vektor PX senkrecht zum Stift ist. Du wirst feststellen das nur für Punkte X in der Tischebene der Vektor PX senkrecht zum Stift ist.

---

Perfekt erklärt, vielen Dank. Sie haben meinen Tag gerettet :)

---

Könnten sie mir bitte ein eine möglichst ausführlich (für Dumme^^) Erklärung für die einzelnen Schritte geben, welche man macht um diese Gleichung in einem Koordinatensystem darzustellen (Die Gleichung, welche auf dem Bild ist). Des Weiteren könnten sie vielleicht die fertige Zeichung der Gleichung als Bild schicken, falls das Bild nicht diese schon zeigt :). Vielen Dank schon einmal.

---

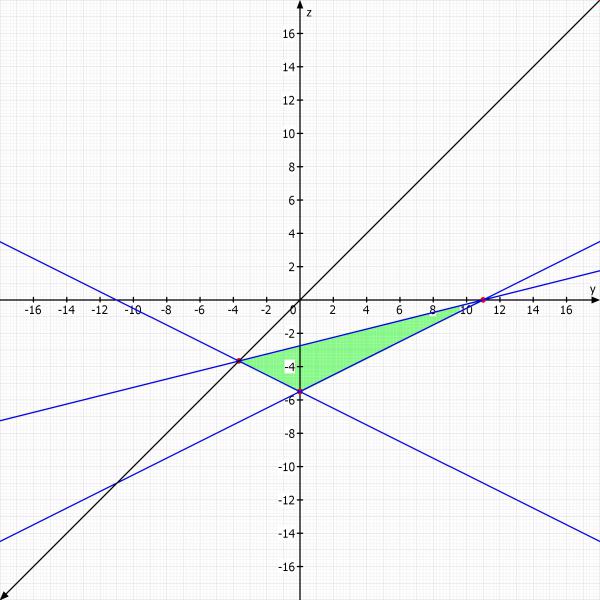
Grundsätzlich sind unbegrenzte Ebenen sehr schwer in ein Koordinatensystem zu zeichnen.

Was du sehr gut machen kannst sind Schnittpunkte mit den Achsen und Schnittgeraden mit den Koordinatenebenen einzuzeichnen.

Dazu formt man die  Gleichung der Ebene in die Koordinatenform um

([2, 0, 3] ⨯ [3, -5, 2]) * (X - [4, -1, 0]) = 0

[15, 5, -10] * (X - [4, -1, 0]) = 0

[15, 5, -10] * X - [15, 5, -10] * [4, -1, 0] = 0

[15, 5, -10] * X = [15, 5, -10] * [4, -1, 0]

15x + 5y - 10z = 55

3·x + y - 2·z = 11

Schnittpunkt mit den Achsen

x = 11/3, y = 11, z = -11/2