Durchschnittliches Wachstum in absoluten Zahlen

Question

Ich habe Probleme mit folgender Aufgabe:

Zwischen 2001 und 2013 entwickelt sich die Anzahl verschickter Nachrichten in einem sozialen Netzwerk nach der Formel f(t)=7+0.7t+0.03 t^2 +0.001 t^3 Mio./Jahr, ( 2001: t=0). Wie groß ist das durchschnittliche Wachstum absolut zwischen 2005 und 2011?

Mein Ansatz bis jetzt:
Funktion ableiten f'(t) = 0.7 + 0.06 t + 0.003 t^2

2005 ist 4 Jahre weg von t=0, 2011 ist 10 Jahre weg von t=0 also (f'(10)-f'(4)) / (10-4)

mit diesem Ansatz komme ich allerdings nicht auf das richtige Ergebnis, was mache ich falsch?

Answer 1

Zur Veranschaulichung

f in Mio / Jahr

( 4 | 10.344 )
( 10 | 18 )
m = Δ y / Δ x = ( y1 - y2 ) / ( x1 - x2 )
m = 1.276 ( Mio / Jahr ) pro jahr

Comments

(f'(10)-f'(4)) / (10-4)
mit diesem Ansatz komme ich allerdings nicht auf das
richtige Ergebnis, was mache ich falsch?

Du hast zunächst die Funktion des Momentanwachstums
/ 1.Ableitung f ´( t ) aufgestellt.
Soweit, so gut.

Hier der Graph ( blau )

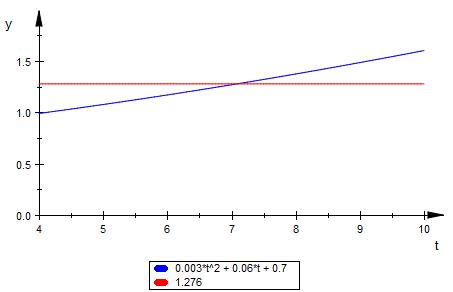Was ist jetzt das mittlere Wachstum ?
Es ist zunächst die Fläche unterhalb von blau
∫ f ´ ( t ) dt zwischen 4 und 10
7.656

Diese Fläche durch 6 ergibt den Durchschnittswert ( rot )
7.656 / 6 = 1.276
und damit genau den Wert der ersten Berechnung.

Denn was ist ∫ f ´ ( t ) dt. Es ist
f ( t ) die Ausgangsgleichung und man kommt wieder auf
( f ( 10 ) - f ( 4 ) ) / ( 10 - 4 )

die Steigung ist :
[ ( Endwert ( y ) - Anfangswert(y) ] / [ Endwert(x) - Anfangswert(x) ]

Das bekannte Steigungsdreieck.

Answer 2

Schau mal ob das so hinkommt.

f(t) = 7 + 0.7·t + 0.03·t^2 + 0.001·t^3

m = (f(10) - f(4)) / (10 - 4) = 1.276 Mio./Jahr^2