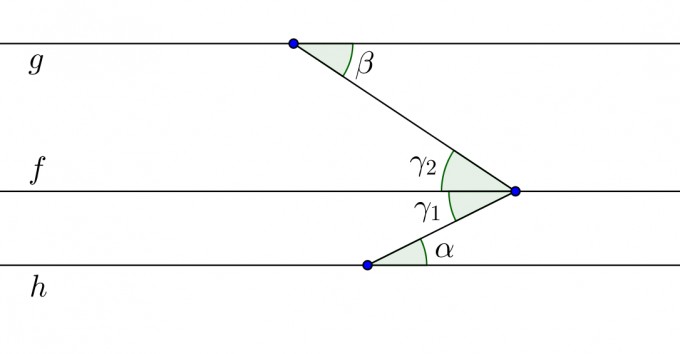
Betrachte eine weitere Gerade \(f\), welche zu \(g\) bzw. \(h\) parallel ist und den Winkel \(\gamma\) in zwei Winkel \(\gamma_1\), \(\gamma_2\) unterteilt.
[spoiler]
Es ist nun \(\gamma = \gamma_1 + \gamma_2\). Wenn man also \(\gamma_1\) und \(\gamma_2\) kennt, kennt man \(\gamma\).
Wie groß sind \(\gamma_1\) bzw. \(\gamma_2\) (in Abhängigkeit von \(\alpha\) und \(\beta\))?
[/spoiler]
[spoiler]
\(\gamma_1\) und \(\alpha\) sind Wechselwinkel, so dass \(\gamma_1 = \alpha\) ist.
\(\gamma_2\) und \(\beta\) sind Wechselwinkel, so dass \(\gamma_2 = \beta\) ist.
Damit ist dann \(\gamma = \gamma_1 + \gamma_2 = \alpha + \beta\).
[/spoiler]