Berechnen des Winkels alpha im Halbkreis, mit zwei Parallelen.

Question

Aufgabe:

Berechnen des Winkels alpha im Halbkreis, mit zwei Parallelen.

Comments

Sind der Winkel mit 35° und die Parallele im Abstand 2 gegeben?

---

Sind der Winkel mit 35° und die Parallele im Abstand 2 gegeben?

Ist das dein Ernst ?

---

Was ist denn überhaupt gegeben ?
r = 3
h = 2

---

"Ist das dein Ernst ?"

Mir sind Zweifel an dem Bild der Aufgabe gekommen, nachdem ich die Zeichnung angefertigt habe:

---

Gegeben ist nur der Winkel mit 35 Grad und die beiden Parallelen. Die Aufgabe sollte mit den Winkelsätzen berechnet werden, ich schaffe es jedoch nicht.

---

Gegeben ist doch auch h = 3.

(Ich meine das h in der Aufgabe, nicht das h bei Benutzer Moliets.)

---

Gegeben ist doch auch h = 3.

Kannst du nicht akzeptieren, dass das nicht so ist ?

---

Dich hat niemand gefragt.

---

So sollte die Skizze wohl aussehen. Es ist f || g. Und f ein Durchmesser des Kreis. Das reicht um $\alpha$ zu bestimmen/berechnen.

---

Wie man aus der Skizze des Fragestellers leicht erkennen kann, beträgt der Winkel   α = 55° .

---

Könntest du erläutern wie du auf dieses Resultat gekommen bist

---

Der Zentrumswinkel zu 35° beträgt 2·35° = 70° , dieser ist 180° - 2α .

---

Vielen dank für die Antwort und die gnaze Hilfe, ich habe es nun verstanden.

Answer 1

sin alpha = Gegenkathete / Hypotenuse h = 2/3

alpha = arcsin 2/3

Comments

alpha = arcsin 2/3

Dürfte wohl kaum die Lösung sein.

---

Wenn Du es nicht besser kannst, Klappe halten.

---

döschwo, wenn du die Aufgabe nicht richtig verstanden hast, dann gifte nicht Leute an, die es besser können.

Der Fragesteller hat zur Aufgabe eine Skizze erstellt. Dabei musste er zwangsläufig die Parallele irgendwo einzeichnen und auch irgendeinen Radius verwenden. Er hat nie von Werten wie 2 LE oder 3 LE gesprochen, aber verlässlich einen (Peripherie-)Winkel von 35° genannt.

---

Er hat verlässlich einen Parallelenabstand von 2 und einen Radius von 3 eingezeichnet. Wenn man der Meinung ist, er habe das falsch gemacht, dann sollte man ihn fragen, ob er es falsch gemacht hat. Ich wünsche einen schönen Abend.

Answer 2

Hallo,

Willkommen in der Mathelounge.

Deine Skizze ist etwas irreführend, da die beiden Parallelen mit einem Abstand von 2 bei einem Radius von 3 eingezeichnet sind. Ich unterstelle mal zwei DInge:

1.) das ist ein Halbkreis, d.h. der Punkt $(0,\,0)$ in dem Koordinatensystem ist der Mittelpunkt des Kreises und

2.) der Winkel links unten im Bild ist mit $35°$ angegeben und die Maße auf der Skizze sind irrelevant.

Dann kann man das ganze so vervollständigen:

Und der gesuchte Winkel $\alpha$ (rot) ist schlicht$$\alpha=90°-35°=55°$$Falls Du Fragen dazu hast, so melde Dich bitte.

Gruß Werner

Comments

Vielen dank für die bessere Skizze, könntest du mit aber erklären wie du auf 90 - 35 kamst?

---

Ich habe es mitlerweile verstanden ist also nichtmehr nötig, trotzdem vielen dank für deine Antwort.

---

könntest du mit aber erklären wie du auf 90 - 35 kamst?

Ich bin so drauf gekommen:

Der gelbe Winkel, den ich oben beim Punkt $B$ eingezeichnet habe, ist genauso Umfangswinkel des Kreises wie die vorgegebenen $35°$. Und da die Tangente (grün) senkrecht auf dem Radius (bzw. Durchmesser) steht, ist die Summe vom gelben und roten Winkel $90°$. Die beiden roten Winkel sind Wechselwinkel an Parallelen und somit gleich.

Eine Alternative bzw. der Satz dazu ist der Sehnentangentenwinkelsatz.

und eine weitere Möglichkeit besteht darin, ein zusätzliches Dreieck in den Kreis einzuzeichnen:

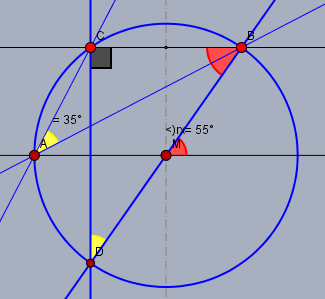
die beiden gelben Winkel sind Umfangswinkel und daher beide $35°$. Im Dreieck $\triangle DBC$ beträgt die Winkelsumme $180°$ und bei $C$ liegen $90°$ an (Thaleskreis), da $DB$ der Durchmesser des Kreises ist.

Die vierte Möglichkeit besteht darin, sich den Mittelpunktswinkel $\angle BMC$ bei $M$ anzusehen.

---

... ist also nicht mehr nötig

zu spät ;-)

---

Bei uns hiess Umfangswinkel noch Peripheriewinkel (?) . Schöne Skizzen.