betrachte dazu ein beliebiges konvexes Vieleck deren Eckpunkte auf dem Einheitskreis liegen:
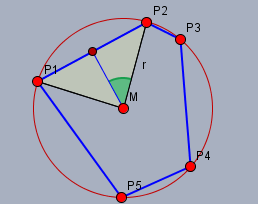
Sein Flächeninhalt \(F\) ist gleich der Summe aller Flächeninhalte \(A_i\) der gleichschenkligen Dreiecke, deren Spitze im Mittelpunkt \(M\) liegt und deren Basis durch eine Kante des Vielecks gebildet werden. Nehme ich den Winkel in der Spitze (z.B. \(\angle \alpha_1 = P_1MP_2\)) als gegeben an, so ist der Flächeninhalt \(A_i\) des \(i\)-ten Dreiecks
$$A_i = r^2 \cdot \cos \frac{\alpha_i}{2} \cdot \sin \frac{\alpha_i}{2} $$
Den Winkel \(\alpha_1/2\) habe ich in der Skizze grün markiert. \(r\) ist der Radius des Kreises, daher in diesem Fall \(r=1\). Die Hautpbedingung ist demnach die (zu maximierende) Fläche \(F\) des Vielecks:
$$F = r^2 \sum_i \cos \frac{\alpha_i}{2} \cdot \sin \frac{\alpha_i}{2} $$ mit der Nebenbedingung $$\sum_i \alpha_i = 2\pi$$ ... muss ja ein Vollkreis sein. Aufstellen der Lagrange-Funktion
$$L(\alpha_i, \lambda) = r^2 \sum_i \cos \frac{\alpha_i}{2} \cdot \sin \frac{\alpha_i}{2} + \lambda\left( \sum_i \alpha_i \space - 2\pi \right)$$ Ableiten nach \(\alpha_i\) und 0-Setzen:
$$\frac{\partial L}{\partial \alpha_i}= r^2 \frac12 \left( \cos^2 \frac{\alpha_i}{2} - \sin^2 \frac{\alpha_i}{2}\right) + \lambda = 0$$ etwas Umformen
$$\sin^2 \frac{\alpha_i}{2} - \frac12= \frac{\lambda}{r^2} $$ und da der Wert für \(\lambda\) unabhängig von \(\alpha_i\) ist, können diese Gleichungen nur genau dann erfüllt sein, wenn alle \(\alpha_i\) gleich groß sind (Bem.: \(\alpha_i \lt \pi\), da \(n \gt 2\)).
Zu den elementaren geometrischen Betrachtungen:
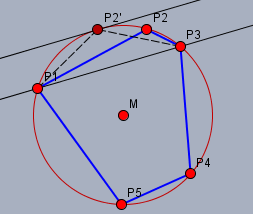
Betrachte einen beliebigen Punkt (z.B. \(P_2\)) und das dazugehörige Dreieck \(\triangle P_1P_3P_2\). Die Frage ist: wie muss man den Punkt \(P_2\) verschieben, damit die Fläche des Dreiecks \(\triangle P_1P_3P_2'\) maximal wird? Da die Grundseite \(P_1P_3\) konstant bleibt, doch offensichtlich so, dass die zu \(P_2'\) gehörige Höhe über \(P_1P_3\) maximal wird. Und dies ist genau dann erfüllt, wenn das Dreieck \(\triangle P_1P_3P_2'\) ein gleichschenliges ist, also die Kanten \(|P_1P_2'|\) und \(|P_2'P_3|\) gleich lang sind. Das gilt natürlich für jeden der Eckpunkte \(P_i\) - also ist die Fläche des Vielecks genau dann maximal, wenn alle Kanten gleich lang sind.
Gruß Werner