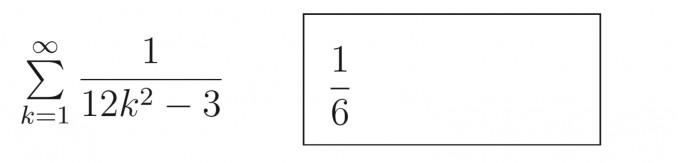Berechnen Sie den Grenzwert der Reihe mit den Summanden 1/(12k^2 - 3)

Question

Mit Rechenweg oder Tipps.!

Ich soll den Grenzwert dieser Reihe berechnen. Die Lösung ist 1/6. Aber ich verstehe nicht ganz, wie ich darauf kommen soll. Ich dachte eigentlich, dass die Reihe harmonisch ist also somit divergent. Wie unterscheide ich die nun?

Außerdem benötige ich Hilfe bei der Berechnung.

Answer 1

1. Klammere 1/3 aus.

2: Berechne Summen der ersten n Glieder nach Ausklammern: 1/3, 2/5; 3/7; 4/9; ... n/(2n+1)

3.der Grenzwert von n/(2n+1) für n gegen unendlich ist 1/2.

4.1/3·1/2=1/6

Answer 2

Mit ein wenig Partialbruchzerlegung bekommst du dies:

$$\sum_{k=1}^{\infty}{\dfrac{1}{12k^2-3}} = \dots = \dfrac{1}{6}\cdot \sum_{k=1}^{\infty}{\left(\dfrac{1}{2k-1}-\dfrac{1}{2k+1}\right)}$$

Comments

Nämlich die schöne Teleskopsumme$$ \dots = \dfrac{1}{6}\cdot {\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dots\right)} = \dfrac{1}{6}.$$