Kugel und Gerade: Gegeben ist eine Gerade g:y+3⋅x−4=0..

Question

Ich brauche bei dieser Aufgabe Hilfe:

Gegeben seien eine Gerade g:y+3⋅x−4=0, ein Kreis K :(x−2)^2+(y−2)^2=r^2.
Wie groß ist der kürzeste Abstand zwischen dem Kreis K und der Geraden g in Abhängigkeit von r?

d(g,K)= ?  wenn r< ?

             ? sonst.

Mein Ansatz wäre das ich die Abstandsformel nehme für Punkt und Gerade um den Abstand zu berechnen.

Ich weiß wenn sich die Gerade mit der Kugel schneidet  dann ist der Abstand =0, aber ich weiß nicht wie ich es in der gewünschten Aufgabe ausdrücken soll..

Kann mir jmd. die Lösung sagen?

Answer 1

Es handelt sich um einen Kreis und nicht um eine Kugel. Ist der Abstand a vom Kreismittelpunkt (2|2) zur Geraden a<r dann schneidet die Gerade den Kreis, ist der Abstand a=r, dann berührt die Gerade den Kreis (Abstand 0) und sonst ist a-r der Abstand der Geraden vom Kreis.

Answer 2

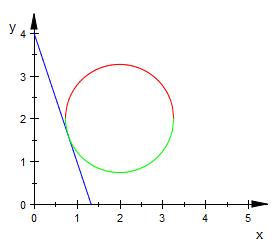
Kreismittelpunkt ( 2 | 2 )
Gerade : y+3⋅x−4=0
g ( x ) = -3x + 4
Steigung : -3
Steigung Normale : - 1 / -3 = 1/3

geht die Normale durch den Kreismittelpunkt
gilt : 2 = 1/3 * 2 + b

b = 4 / 3
n ( x ) = 1/3 * x + 4/3

Schnittpunkt g mit n
-3x + 4 = 1/3 * x + 4/3
-3*3 / 3 * x + 4 = 1/3 * x + 4/3
- 10 / 3 * x = - 8 / 3
x = 0.8

y = -3x + 4
y = -3 * 0.8 + 4
y = 1.6
S ( 0.8 | 1.6 )

Abstand Kreismittelpunkt / Schnittpunkt
√ [ ( 2 - 0.8 )^2  + ( 2 - 1.6 )^2 ]
√ [ 1.44 + 0.16 ]
1.265

Bei einem Radius von 1.265 ist die
Gearde g eine Tangente und der Abstand
ist null.

So mache zunächst einmal Schluß