Newtonverfahren für Logarithmen. Wie das Verfahren als Exponentialfunktion graphisch darstellen?

Question

Wie stelle ich das Newton-Verfahren zum Logarithmieren graphisch dar? Die Exponentialfunktion berührt ja die x-Achse nicht und daher gibt es auch keine Nullstelle wie bei der Berechnung von Wurzeln! Das heißt eigentlich müsste es nicht gehen. Aber es geht eben doch und daher muss man es auch irgendwie graphisch darstellen können. Ich weiß aber nicht wie! Vielleicht kann mir jemand helfen.

Die Formel lautet: Xn+1 = Xn - ((e^x - n)/e^x).

Für eine Erläuterung wäre ich dankbar!

Answer 1

du hast ja die Exponentialfunktion $$ f(x)=e^x-a,\quad a>0 $$. Du willst ein bestmögliches x haben, damit du den Wert a so gut wie möglich annähern kannst. Möglich ist das zum Beispiel durch das von dir angesprochene Newtonverfahren. Dann hat man also

$$ x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}=x_n-\frac{e^{x_n}-a}{e^{x_n}} $$

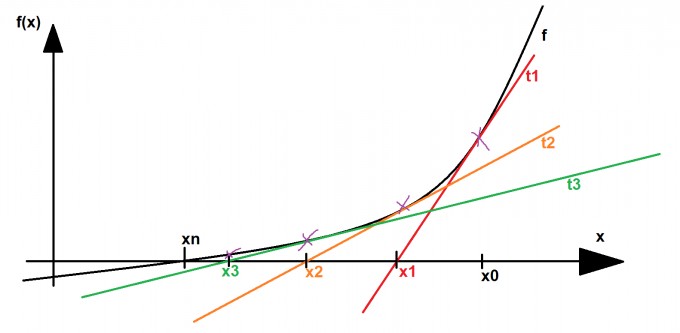
Nur ist das jetzt eine rekursive Folge, also eine Folge die von ihrem Vorgänger abhängig ist. Es ist generell nicht immer möglich aus einer rekursiven Bildungsvorschrift eine explizite zu bekommen. Außerdem hängt hier deine Folge sehr von deinem Startwert x₀ ab. Somit fällt auch deine entstehende Folge entsprechend anders aus, aber sie konvergiert für n→∞ gegen einen festen Wert, hier $$ \ln(a) $$.

Fazit, du kannst diesen Sachverhalt nicht als Kurve graphisch darstellen, sondern nur die Tangente an der Stelle x_n , die an f liegt. Und je öfter du das Newetonverfahren anwendest, desto näher liegt die Nullstelle der n-ten Tangente gerade an der von f.