Was gemeint mit den Symmetrieeigenschaften, oder was gehört hier zu Symmetrieeigenschaften?

Question

Welche Symmetreieigenschaften haben die Graphen?

f(x)= 1.5*x^2

f(x)=-1.5*x^2

f(x)=0.3*x^2

f(x)=-0.3*x^2

kann man so antworten

Symmetrieeigenschaften

No

1) in Richtung y Achse  gestreckt ,und y Achse symmetrisch

2) an x Achse gespiegelt und und  an  negativen y Achse symmetrisch

3) in Richtung y Achse  geschtauch ,und y Achse symmetrisch

4) an x Achse gespiegelt und  an negativen y Achse symmetrisch

Answer 1

Ich würde als Antwort schreiben:

Die Funktionen sind achsensymmetrisch zur y-Achse.

Die Streckung und Stauchung ändert nix an der Symmetrie der Parabel.

Answer 2

du könntest es auch so betrachten. Du betrachtest eine Funktionsscharr der Form $$ f_a(x)=a\cdot x^2, \quad a\in \mathbb{R}.$$

Jetzt kannst du ja die Symmetrie daran prüfen.

Achsensymmetrie zur y-Achse $$ f(x)=f(-x) $$

Punktsymmetrie zum Koordinatenursprung $$ f(x)=-f(x) $$

In beide Bedingungsformeln setzt du deine Funktionsscharr ein. Und dort, wo Gleichheit resultiert (geht nur bei einen von den beiden), ist dann auch die Eigenschaft, die für die Funktion gilt. Und somit hast du das sogar für alle quadratischen Funktionen der Form $$ f_a(x)=a\cdot x^2 $$ gezeigt.

Comments

leider nicht genau verstahnde , was meinst du mit Funktionsscharr und wie so  f(x)=−f(x)?

danke

---

f(x)=-f(x)

ist falsch bei Punktsymmetrie zum Koordinatenursprung.

Es muss

f(x) = - f(-x)

heissen.

---

@ TR    Oh, danke für den Hinweis.

@ ismail

Eine Funktionsscharr ist eine Menge von Funktionen mit abhängigen Parameter(n). Bei dir wäre a ein Parameter. Dieser kann beliebig gewählt sein. Zum Beispiel nur in einem bestimmten Intervall oder eben alle reellen Zahlen.

Das hier wäre zum Beipiel eine Funktionsscharr mit $$ a∈[-5;-4,5;-4;...,4;4,5;5] $$

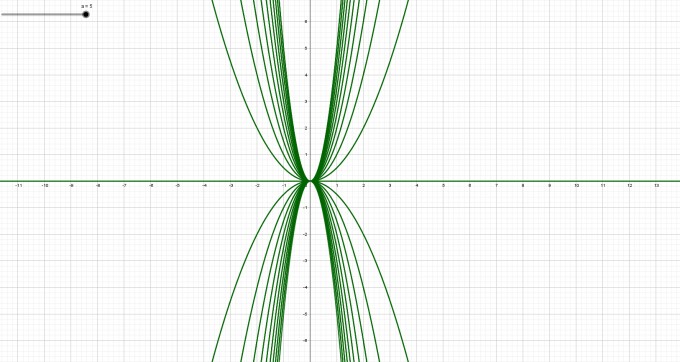
Und wie du schon daran erkennen kannst, erfüllen all diese Funktionen die Achsensymmetrie zur y-Achse.

Nur sind das nicht alle, da a nur aus einem Intervall gewählt wurde im 0,5 Schritt.

Answer 3

Alle Funktionen sind Parabeln.

Parabeln sind achsensymmetrisch zur
x - Stelle des Scheitelpunkts.

Siehe deine Grafiken.

Comments

hallo , du meinst  jede Parabel an x A an hse gespiegelt ?

---

Punktsymmetrie zum Koordinatenursprung

f(x)=−f(x) was bedeutet hier? und stimmt das?

---

Ismael, wie schonmal gesagt fehlt es dir an
Basiswissen.

Du fragst immer dasselbe.

Schau dir einmal deine Grafik einer Parabel an.

Für eine zur y-Achse symmetrische
Parabel gilt :
f ( 4 ) = f ( -4 )
f ( 2 ) = f (- 2)
f ( x ) = f (-x )

f ( x ) = 1.5 * x^2
f ( -x ) = 1.5 * (-x)^2 = 1.5 * x^2
f ( x ) = f (-x )

Schau dir Lernvideos über die Symmetrie
von Funktionen an.

---

ich versteh e , aber dich aber nur

das (Parabeln sind achsensymmetrisch zur
x - Stelle des Scheitelpunkts.)habe nicht genau verstanden ws du meinst: ich weiß parabel symmetrisch zu y Achse 

also f(-2^2) =f(2^2)

        4= 4

---

also f(-2^{2}) =f(2^{2})

        4= 4

Nicht ganz!

Genauer:

f(x) = x^2

f(-2) =?= f(2)

(-2)^{2}=?= 2^{2}   Klammern um -2 und um 2 und kein f verwenden :)

        4= 4 stimmt!

Richtig.

In der Schule wird aber eher erwartet, dass du Symmetrieachse einer Parabel von Auge erkennst. Man kann den Graphen an einer Symmetrieachse falten. Die beiden Parabeläste liegen dann aufeinander.

---

Ismael, du mußt dir Lernvideos anschauen.

Du mußt dir ein komplettes Basiswissen aneignen.

mfg Georg

---

danke ,gern empfehlst du bestimmmten Vedios oder ein Buch, ich ler eine von einem Buch .