In einem Zoo befindet sich ein Käfig mit 28 Wellensittichen.
- 9 Blaue
- 7 Gelbe
- 12 Olive
Kinder dürfen einen Wellensittich auf der Hand tragen. Dazu nimmt der Wärter zufällig einen aus dem Käfig, welcher nacher wieder dorthin kommt, bevor der nächste Vogel herausgenommen wird.
Mit welcher Wahrscheinlichkeit...
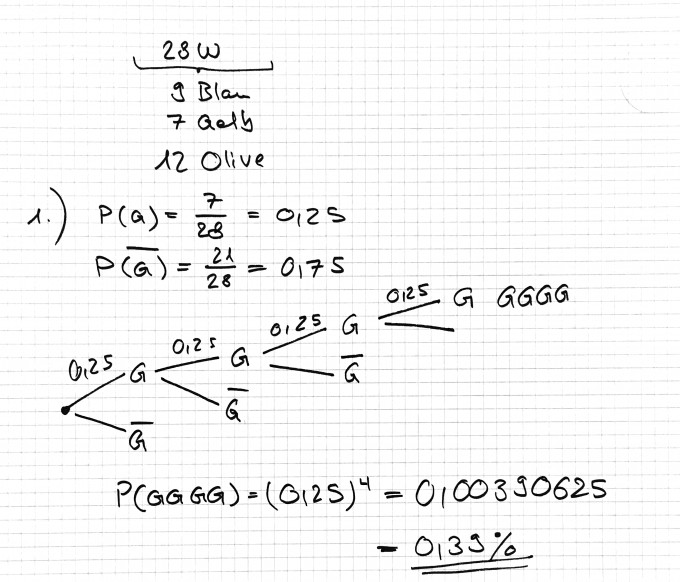
...(1) werden nacheinander 4 gelbe Wellensittiche herausgenommen?
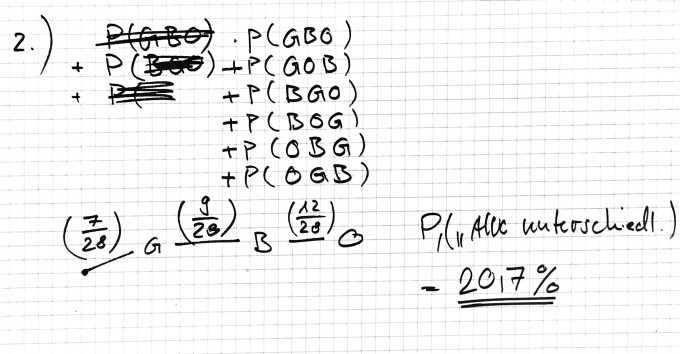
...(2) sind 3 nacheinander herausgenommene Vögel alle unterschiedlicher Farbe?
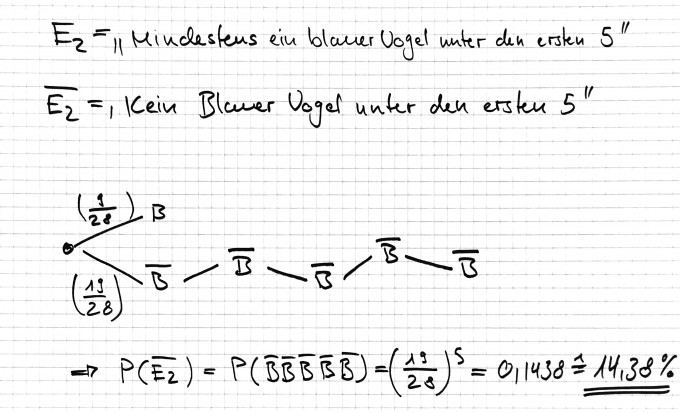
...(3) befindet mindestens ein blauer Vogel unter den ersten 5 herausgenommenen Vögel?
----------------------------- Mein Vorgehen ---------------------------------
(1) Hier arbeite ich mit einem Baumdiagramm und mit der Wahrscheinlichkeit P(G) = "Gelb" seinem Gegenereignis.
LSG: 0.39%
(2) Hier liste ich alle Möglichkeiten für drei Unterschiedliche Ziehungen auf und berechne deren Wahrschinlichkeiten und addiere diese dann zusammen. Diese ergeben mir dann die Wahrscheinlichkeit für P(Alle unterschiedlich).
LSG: 20.7%
(3) Ich arbeite mit dem Gegenereignis von
E2 = "Mindestens ein Blauer Vogel unter den ersten 5".
Komplement v. E2 =" Kein blauer Vogel unter den ersten 5 herausgezogenen".
LSG: 14,38%
Frage:
Da es zu dieser Aufgabe keine Lösungen gibt (alte Prüfung) würde es mich freuen, wenn jemand das mal anschauen könnte und mir ein Feedback geben kann.