Über dem horizontalen Strich darfst du hinschreiben was du willst.
Unter dem horizontalen Strich musst du hinschreiben, was du daraus folgerst. Du musst dann natürlich in der rechten Spalte angeben, warum du das folgern darfst. Die Regeln, nach denen du folgern darfst, stehen im Abschnitt Rules. Links sind Zeilennummern. Rechts vom senkrechten Strich ist ein Beweisausschnitt. In der letzten Zeile jeder Regel steht dann rechts, wie du diese Regel in die Spalte Justification einträgst.
Ein weiteres gefundenes Beispiel in deren Blog mit richtigem Beweis:
1. Es gilt A∨B (laut Prämisse)
2. Es gilt ¬A (laut Prämisse)
3. Angenommen es gilt A
4. Wegen Regel ⊥I (siehe Rules for Cambridge) bezogen auf Zeile 2 und 3 ist das ein Widerspruch.
5. Regel ⊥E (ex falso quodlibet) angewendet auf Zeile 4 ergibt B.
6. Angenommen es gilt B (dann gilt B, was man aber dann nicht unter dem Strich folgern muss)
7. Wegen Regel ∨E (Basic Rules, Definition von ∨) ist B damit bewiesen, weil unter den gegebenen Prämisen B aus A folgt und B aus B folgt.
Versuch damit mal, folgenden Beweis von Q→(Q∧¬Q) ∴ ¬Q nachzuvollziehen.
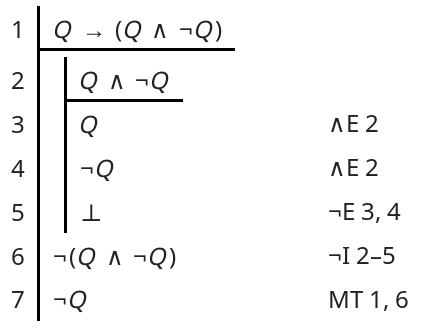
Das sind eher Aufgaben und keine Beispiele. Links vom ∴ stehen die Voraussetzungen. Das sind die Zeilen über dem Strich im Beweis. Rechts vom ∴ steht, was du beweisen sollst. Das sollte dann auch die letzte Zeile unterm Strich in deinem Beweis sein.