hier mal eine Skizze zur Orientierung.
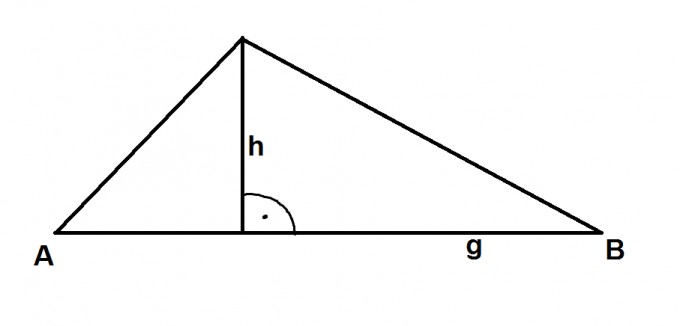
Bestimme anhand von ausgewählten (geeignete) Punkten alle drei Geradengleichungen. Dann legst du eine Seite als Grundseite fest. Die Länge davon bekommst du durch den Satz des Phythagoras, also
$$ d(A;B)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2} $$
Jetzt musst du die Höhe bestimmen. Dafür musst du den Schnittpunkt der beiden anderen Geraden bestimmen (gleichsetzen) und den Punkt auf der Grundseite. Dafür stellst du eine Gerade h auf, die senkrecht zu g steht und durch den Schnittpunkt der beiden anderen Gerade geht. Dann auch hier h=g und du hast den Schnittpunkt auf der Grundseite. Jetzt wieder die Abstandsformel verwendet und du hast die Länge der Höhe. Dann noch
$$ A_D=\frac{g\cdot h}{2} $$ und fretig. :)