Wendetangente von e-Funktion f(x) = 10x*e^{1/2x}

Question

die funktion lautet 10x*e^{1/2 x} 

die 1/2 x steht im Exponenten

Bestimmen Sie die Gleichung der Tangente im Wendepunkt Bestimmen sie an welcher Stelle die Wendetangente die x achse schneidet.

Answer 1

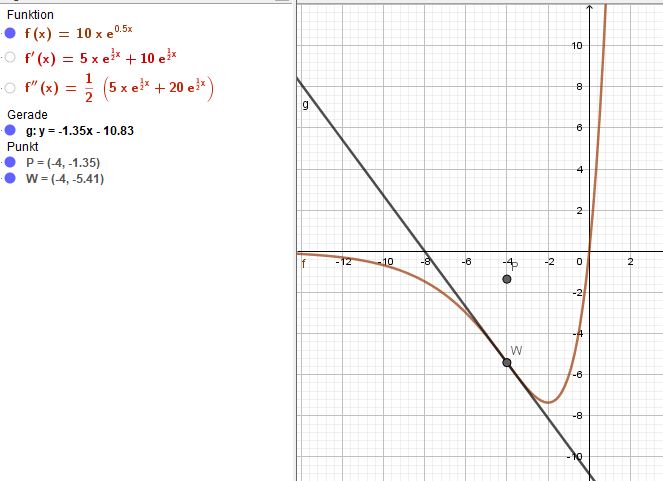
$$f(x)=10x\cdot e^{\frac{1}{2}x}\\f'(x)=(5x+10)\cdot e^{\frac{1}{2}x}\\f''(x)=(2,5x+10)\cdot e^{\frac{1}{2}x}$$

Die 2. Ableitung = 0 ergibt für x den Punkt W(-4|-5,41)

Für die Tangente berechnest du die Steigung von W: f'(-4) = -1,35

Diesen Wert und die Koordinaten des Punktes in die allgemeine Tangentengleichung t(x) = mx + b ergibt b= -10,83

Gruß, Silvia

Comments

kannst du das bitte vorrechnen ?´

---

Was genau möchtest du vorgerechnet haben?

---

wie man auf den Wendepunkt W(-4|-5,41) kommt wegen der e funktion macht es mir probleme

---

Aber die Ableitungen kannst du bilden?

---

ja das kann ich

---

OK, dann schreibe ich dir das mal ausführlich auf und scanne es ein.

---

Ich hoffe, damit kannst du weiterarbeiten.

---

ich kann nicht alles sehen was du geschrieben hast

---

OK, ich schreibe es nochmal.

---

So, jetzt sollte alles lesbar sein.

 

...auch wenn ich das Bild nicht gedreht bekomme

---

danke dir mir ist grad aufgefallen das ich einen riesen fehler gemacht habe die funktion lautet eigentlich 10x e ^ -1/2x

ein - hat gefehlt

---

ich habe dann -1,3533x +0 raus als tangente

---

Der Wendepunkt ist dann bei (4|5,413) und die Gleichung der Tangente lautet

t(x)=-1,353x+10,83

 

Answer 2

Hallo

1. 2 mal ableiten nach Produkt +Kettenregel, dann f''(x)=0 um den Wendepunkt zu finden. dann die x- Koordinate des Wendepunktes in f'(x) einsetzen, ergibt die Steigung der Tangente, die dann noch durch den Wendepunkt gehen muss.

Was an den Schritten kannst du nicht? zur kontrolle  Wendepunkt bei (-4, 5.413)

Gruß lul

Comments

wie man auf den Wendepunkt W(-4|-5,41) kommt wegen der e funktion macht es mir probleme