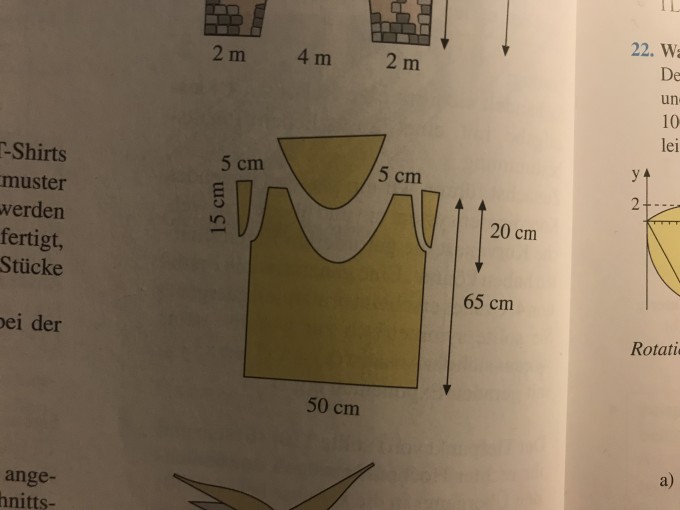
Eine Konfektionsfirma will T-Shirts nach nebenstehendem Schnittmuster herstellen. Die Stoffrohlinge werden zunächst in Rechtecksform gefertigt, dann werden parabelförmige Stücke herausgeschnitten. Welchen prozentangeil hat hierbei der Verschnitt?
Ich habe dazu erstmal das T-Shirt in Arm und Halsbereich aufgeteilt.
Arm: P (5/15)
f(x)=ax^2
15=a*5^2
a=15/25 = 3/5
Hals: P (15/20)
f(x)= ax^2
20=a*15^2
4/45= a
Das Ergebnis liegt im Bereich von 15%
Weiter komme ich leider nicht und ich weiß auch nicht, ob das Sinn ergibt. Wäre froh, wenn der Rest gelöst werden würde, da ich einfach nicht weiter komme.