Schnittpunkt f(x) = (x+3)^2-5 mit Geraden g: 2y-4x = 3

Question

Hi brauche Hilfe,

 

gegeben ist die Formel f(x)= (x+3)²-5

 

gesucht: Schnittpunkt mit der Geraden g: 2y-4x=3

und die Darstellung

 

vielen Dank schon mal

Answer 1

Hi,

die Gerade umgeformt:

2y-4x = 3

2y = 3+4x

y = 2x+1,5

 

Gleichsetzen mit der Parabel:

(x+3)^2-5 = 2x+1,5

x^2+6x+9-5 = 2x+1,5    |-2x-1,5

x^2+4,5x+2,5 = 0           |pq-Formel

x₁ = -2-√(3/2) und x₂ = -2+√(3/2)

 

Das dann noch in die Gerade einsetzen um den Schnittpunkt zu finden:

S₁(-2-√(3/2) | -5/2-√6) und S₂(-2+√(3/2) | -5/2+√6)

S₁(-3,22|-4,95) und S₂(-0,78|-0,05)

 

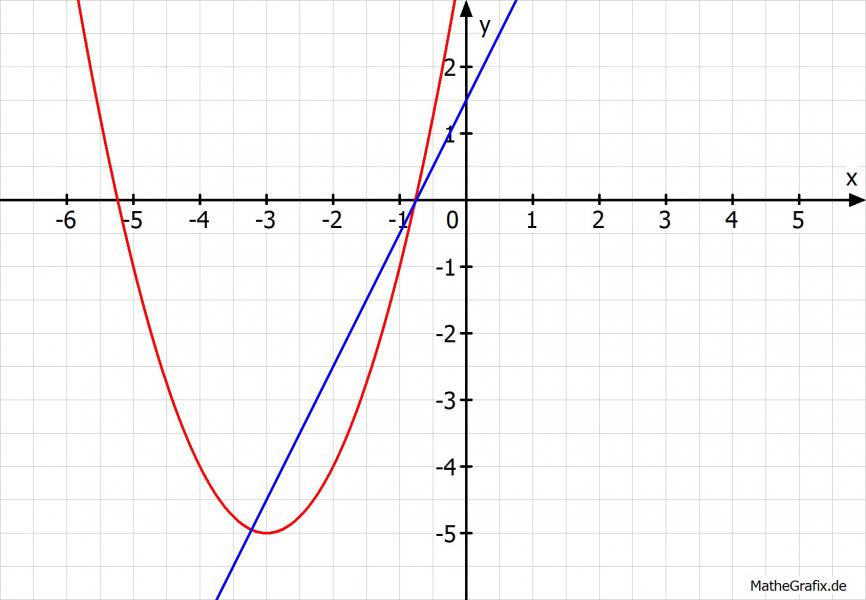
Grüße