Geradengleichung, Schnittpunkt zweier Geraden

Question

Gegeben sind die beiden Geraden g und h mit den Gleichungen g(x) = 2x + 3 und h(x) = mx - 3, D = ℝ, m ∈ ℝ. Bestimmen Sie alle Werte von m, für die der Schnittpunkt der beiden Geraden g und h im III. Quadranten des Koordinatensystems und oberhalb der Geraden mit der Gleichung y = -3 liegt.

Ich weiß nicht wie ich für die Steigung von h(x) vorgehen soll.

Answer 1

Ich weiß ja nicht, ob Du schon die Lösung hast aber einen Tipp gebe ich mal ab:

Es ist mehr Logikrätsel als Rechenaufgabe, du gerechnet müssen zwei Werte, wobei einer zur Berechnung des zweiten gebraucht wird. Schnittpunkte  oder Schnittstellen selbst brauchst Du gar nicht. Dein Ergebnis wird so aussehen: [kleiner Wert] < m < [großer Wert], Du musst also diese zwei Werte angeben.

[großer Wert] steht in der Aufgabe versteckt drin. [kleiner Wert] wird über angedeuteten Zweischritt ermittelt.

Soweit der Tipp, wenn Du doch eine Lösung brauchst, reiche ich sie gerne nach. Ach und zeichne Dir das mit allen Bekannten  einfach mal auf, dann sieht man die Lösung auch, wenn man die möglichen Geraden h(x_m) mit dem Geodreieck/Lineal andeutet.

Comments

Danke für den ausführlichen Tipp.

Hat mir sicher einen guten Ansatz gegeben, leider komme ich dennoch nicht auf die Steigung / ein Ergebnis, bräuchte also doch die Lösung.

---

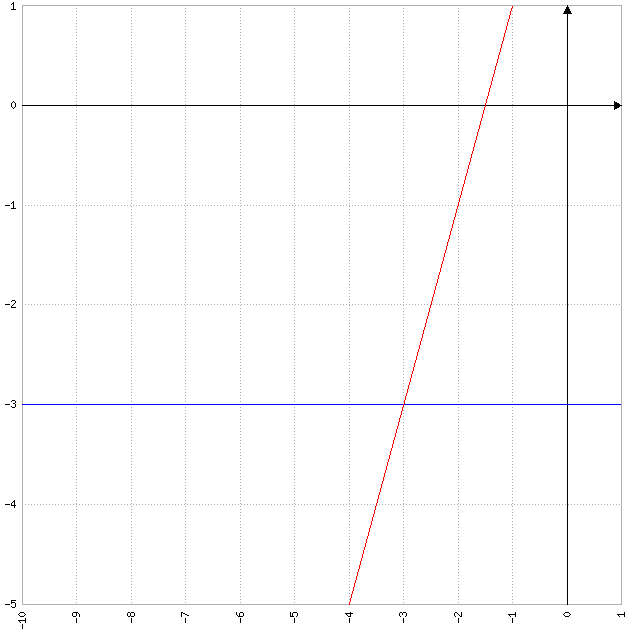
rot ist g(x)

blau ist y=-3

Der Abschnitt auf dem die gesuchten Schnittpunkte liegen können sind zwischen den Schnittpunkten von g(x) und y=-3 und der x-Achse, da dieser Bereich im Quadrant 3 und oberhalb y=-3 liegt.

Wenn Du in h(x) den Wert 0 für m einsetzt : h(x)=0*x-3 ist das gleich y=-3. Wird m > 0 liegt der Schnittpunkt unterhalb y=-3 also sind nur Werte kleiner als 0 für m gesucht, somit hast du die erste Grenze: m<0

Der Schnittpunkt von g(x) mit der x-Achse ist ermittelbar, wenn der Funktionswert =0 ist:

g(x)=0

0=2x+3 ;nach x umstellen

x=-1,5

Daraus ergibt sich als erster nicht gültiger Schnittpunkt (-1,5/0) den setzt Du in h(x) ein und ermittelst m:

h(-1,5)=0

0=-1,5m-3 ;nach m umstellen

m=-2

Jetzt hast Du die beiden gerade nicht mehr gültigen Werte für m, damit die geforderten Eigenschaften der Schnittpunkte wahr sind. m muss größer als -2 und kleiner als 0 sein, oder schöner:

-2 < m < 0

Answer 2

Schnittpunkt zweier Geraden

Gleichsetzen, nach x auflösen, einsetzen.