Betrachte zunächst folgende Skizze.
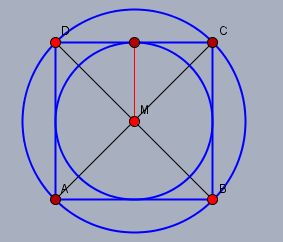
Der äußere Kreis habe den Radius \(r_0\). Das Quadrat \(ABCD\) habe die Kantenlänge \(a_0\). Seine Diagonale \(d_0\)(schwarz) hat nach Pythagoras die Länge \(d_0 = a_0 \sqrt{2}\). Die Diagonale ist aber auch gleich zweimal der Radius \(r_0\): $$d_0 = a_0 \sqrt{2} = 2 r_0 \quad \rightarrow a_0 = r_0 \sqrt{2}$$ Allgemein gilt: $$a_i = r_i \sqrt{2}$$ Die Kantenlänge \(a_0\) des Quadrats ist identisch mit dem halben Radius \(r_1\) (rot) des inneren Kreises \(a_0 = 2r_1\). Bzw. allgemein: $$r_i = \frac12 a_{i-1}$$ Die rekursive Formel für die Radien der Kreise lautet demnach: $$r_i = \frac12 a_{i-1} =r_{i-1} \frac12 \sqrt{2} \quad \Rightarrow r_i = r_0 \left( \frac12 \sqrt{2}\right)^i$$ Und für die Kantenlängen gilt das gleiche: $$a_i = r_i \sqrt{2} = a_{i-1} \frac12 \sqrt{2} \quad \rightarrow a_i = a_0 \left( \frac12 \sqrt{2}\right)^i$$
a) Die Summe der Flächeninhalte aller Kreise ist (s. geometrische Reihe)
$$ \sum A_K = \sum \pi r_i^2 = \cancel{\pi \sum r_0 q^i = \pi \frac{r_0}{1 - q} = \frac{\pi r_0}{1 - \frac12 \sqrt{2}} = \pi r_0 (2+\sqrt{2}) } \\ \space = \pi \sum_{i=0}^{\infty} \left( r_0 \left( \frac12 \sqrt{2}\right)^i \right)^2 = \pi r_0^2 \sum_{i=0}^{\infty} \left( \frac12 \right)^i = \pi r_0^2 \frac{1}{1-\frac12} = 2 \pi r_0^2$$
b) die Summe der Flächeninhalte aller Quadrate
$$ \sum A_Q = \sum a_i^2 = \cancel{ \sum a_0 q^i = r_0 \sqrt{2} \sum q^i = \frac{r_0 \sqrt{2}}{1- \frac12 \sqrt{2}} = 2 r_0 (1 + \sqrt{2}) } \\ \space = \sum_{i=0}^{\infty} \left( a_0 \left( \frac12 \sqrt{2} \right) ^i \right)^2 = a_0^2 \sum_{i=0}^{\infty} \left( \frac12\right)^i = 2a_0^2 = 4 r_0^2$$
c) die Summe der Umfänge aller Kreise
$$\sum U_K = \sum 2\pi r_i = 2\pi \sum r_0 q^i = \dots $$ ... den Rest schaffst Du alleine - oder?
Gruß Werner