der Hauptsatz der differential-und Integralrechnung

Question

Hallo

Ich habe hier ein Beispiel vor mir, die lautet:

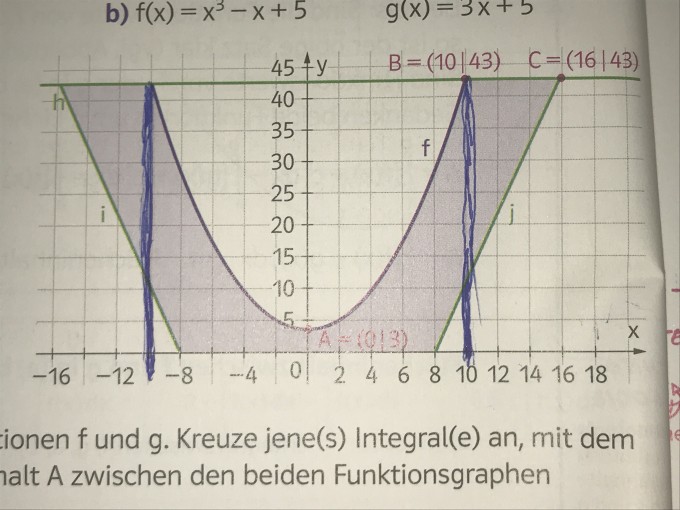
In der Abbildung ist ein Schnitt durch eine Vase(Masse in cm) abgebildet. (Foto)

Berechne den Flächeninhalt, der durch den Graphen der Funktion f mit f(x)= ax^2+b, der x-Achse sowie den Geraden h,i und h begrenzt wird. Bei der Lösung sollte 498,67 rauskommen.

Meine Frage ist, wie ich das berechne und vorgehen muss. Ich wäre dankbar für eine kurze Erklärung und einen Rechenvorgang !

Lg 

Answer 1

da f achsensymmetrisch zur y-Achse ist, genügt der Ansatz $$ f(x)=ax^2+c$$ Da f(0)=3, folgt c=3. Berechne jetzt nur noch a mit dem Punkt (10/43). Da du ein Trapez als gesamte Fläche hast, kannst du so erstmal den Flächeninhalt davon berechen. Die Höhe ist h=43 und die Länge der waagerechte Strecke (die Breite) in der mitte bei y=22,5 ist l=16. Damit erhältst du den gesamten Flächeninhalt.

Jetzt musst du noch die parabelförmige Fläche abziehen, indem du den Flächeninhalt zwischen der waagerechten Gerade w(x)=43 und f von -10 bis 10 berechnest. Dafür bildest du eine Differenzenfunktion. Ich nenne sie mal d(x)=f(x)-w(x). Dann berechnest du damit:

$$ \int_{-10}^{10} f(x)-w(x)\ dx $$