Umfrage über das Schwarzfahren kombiniert mit Laplace-Würfel

Question

Schon mal schwarz gefahren?

Damit der Fahrgast sicher ist, dass ihm aus der Antwort "ja" keine Nachteile entstehen können, schlagen die Verkehrsbetriebe folgendes Verfahren vor: Der Befragte würfelt einen Laplace-Würfel. Die gewürfelte Augenzahl sieht nur er! Bei einer Augenzahl unter 5, soll er die Frage wahrheitsgemäß beantworten. Bei einer 5 soll er immer mit "ja" und bei einer 6 immer mit "nein" antworten. Es soll davon ausgegeangen werden, dass alle Befragte das Verfahren korrekt befolgen.

a) Wie viele "ja"-Antworten hat man 100 Befragten und einem Schwarzfahreranteil von 20% zu erwarten?

Mit welcher Wahrscheinlichkeit ist dann ein Fahrgast, der mit "ja" antwortet, schon einmal schwarz gefahren?

b) Wie groß ist der Schwarzfahreranteil p, wenn 22,8% der Befragten mit "ja" antworten?

Ich komme zum folgenden Ergebnis:

P("ja") = 4/6 * 2/10 + 1/6 = 0,3 = 30%. Es sind also 30 "ja"-Antworten zu erwarten.

P("nein") = 4/6 * 8/10 +1/6 = 0,7 = 70%

In einer Vierfeldertafel sieht die Verteilung so aus:

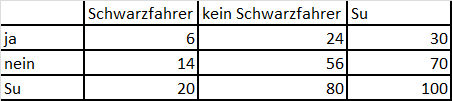
Somit ergibt sich P_ja(S)=6/30=0,2=20%

b) p= 22,8/30 * 20 =15,2%. Dann gibt es 15,2% Schwarzfahrer statt der geschätzten 20%.

Sind mein Folgerungen richtig? Eine Bestätigung oder ggf. Korrektur wäre nett.

Answer 1

Meine Antwort würde wie folgt lauten:

Comments

Vielen Dank für die Antwort! Dann stimmt wohl meine Vierfeldertafel auch nicht; wie würde denn die richtige Verteilung aussehen?

---

	Schwarzfahrer	Kein Schwarzfahrer	∑
Ja	1/6	2/15	0.3
Nein	1/30	2/3	0.7
∑	0.2	0.8	1

P(Schwarzfahrer | Ja) = (1/6) / (0.3) = 5/9 = 0.5556
Da habe ich mich oben also verrechnet.

Das Baumdiagramm sieht so aus:

---

Sorry, dass ich nerve. Ich blicke immer noch nicht ganz durch. Klar ist mir, dass es 30% Ja-Sager und 70% Nein-Sager gibt. Vorgegeben ist auch der Schwarzfahreranteil von 20% und 80% der ehrlichen Kunden. Doch wie kommst du bei deinem inversen Baumdiagramm auf 5/6 und 1/6 für J und N, da ich doch nur weiß, welche Verteilung es beim Würfeln gibt? Ich habe 1/6, die immer ja sagen (bei einer 5) und 1/6, die immer nein sagen (bei einer 6) und dann habe ich 4/6 der Befragten, die wahrheitsgemäß antworten.

2. Frage: Die Antwort zu b) bleibt von deiner Korrektur unberührt - oder?

---

5/6 = 4/6 + 1/6

Also 4/6 die ehrlich antworten und 1/6 die aufgrund des Wurfergebnisses es so angeben mussten.

Du kannst also im Grunde im Zweiten Schritt auch jeweils 3 Pfade machen Wurf 1-4, 5, 6. Und darunter dann das Ergebnis.

Ich habe das hier nur Zusammengefasst.