Komplexe Zahlen - Radizieren?

Question

in der Mathevorlesung hatten wir das Thema "komplexe Zahlen" und haben uns heute mit dem "Radizieren" von kompelxen Zahlen beschäftigt und ein kleines Beispiel gemacht, welches ich ab er nicht so gut verstanden habe und der Professor auch nicht so gut erklärt hat.

Ich habe euch meine Aufgabe notiert. Die Aufgabe ist bereits gelöst, nur verstehe ich die Rechenwege nicht ganz.

Im Anhang seht ihr meine Aufgabe.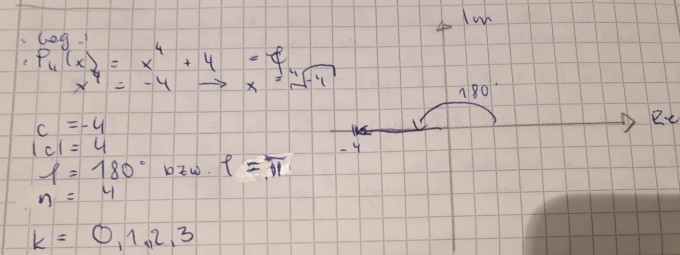 

Die vier Zeilen mit Wurzel 2 als Betrag, gehören jeweils zu den Zeilen da oben, da ich nicht genug Platz hatte. Ich glaube die erste Zeile mit Wurzel 2 gehört zu W0/1, die zweite zu w2 und so weiter. Weiß ich gerade selber nicht genau.

Wenn ich das mit dem Cosinus und Sinus jeweils eingebe in den Taschenrechner, erhalte ich Werte mit denen ich nicht weiß was ich mit anfangen soll. Beispielsweise die erste Zeile mit Wurzel 2: (cos(pi/4) + j*sin(pi/4)) = 1+ j

Beispielsweise  für cos( π/4)  = √2 / 2 .  Keine Ahnung..  könntet ihr mir bitte einfach das Thema bzw. diese Aufgabe, wenn es geht, etwas ausführlicher erklären.

Comments

Ich weiß ich habe die Frage wahrscheinlich nicht ausreichend erklärt, deshalb bitte ich euch, diese Frage irgendwie selber zu verinnerlichen und versuchen zu verstehen, worauf ich hinaus möchte bitte..

---

Bei dem ein oder anderen Schritt bitte etwas ausführlicher erklären.. verzweifle teilweise.

Answer 1

z^4= -4

Berechnung in 3 Schritten:

1. Betrag bilden :

|z1|= √ (Realteil)^2 +(Imaginärteil)^2) =√(-4)^2+0^2) =4

2. Winkel berechnen:

tan( φ)= (Imaginärteil/Realteil)= 0/(-4)= 0

φ= π (2.Quadrant) , n=4

3.Einsetzen in die allgemeine Formel:

z_k= |z₁|^{1/n} e^{i(φ+2kπ)/n} ; k=(0,1,2,3)

Beispiel for k=0:

z₀= 4^{1/4} e^ (i π)/4 = √2 *e^ (i π)/4

z₀= √2 (cos(π/4) +i sin(π/4))

z₀= √2(√2/2 + i √2/2)

z₀=  1+i

usw.