Aufgabe für Bedingte Wahrscheinlichkeit. Weisse, graue und schwarze Urne mit farbigen Steinen.

Question

Aufgabe für Bedingte Wahrscheinlichkeit:

Gegeben sind eine weiße, einen graue und eine schwarze Urne, die jeweils mit 36 Steinen in den Farben Rot und Blau gefüllt sind. Bei der Ziehung aus einer Urne soll jeder Stein die Wahrscheinlichkeit \( \frac{1}{36} \) haben. Dabei enthält die weiße Urne 6 rote und 30 blaue Steine, die graue Urne 18 rote und 18 blaue und die schwarze Urne 30 rote und 6 blaue. Der folgende Prozess beschreibt die Ziehung eines Steins: Zuerst wird eine Zahl \( a \in \) \( \{1,2, \ldots, 6\} \) gewürfelt (gleichverteilt). Bei \( a=1 \) zieht man einen Stein aus der weißen, bei \( a \in\{2,3\} \) einen Stein aus der grauen und sonst einen Stein aus der schwarzen Urne. Wir bezeichnen mit \( W, G, S \) die Ereignisse, dass der Stein aus der weißen, grauen bzw. schwarzen Urne gezogen wurde und mit \( R, B \) die Ereignisse, dass am Ende ein roter bzw. blauer Stein gezogen wurde.

a) Untersuchen Sie, ob die Ereignisse \( B \) und \( G \) unabhängig sind.

b) Bestimmen Sie unter Voraussetzung von Ereignis \( R \) die bedingten Wahrscheinlichkeiten von \( W, G \) und \( S \).

c) Wie müsste man die Anzahl der roten und blauen Steine in der schwarzen Urne ändern, damit (unter Beibehaltung aller anderen Regeln) die Ereignisse \( G \) und \( R \) unabhängig werden.

Answer 1

hello!

erstmal ein bildchen, für die berechnung von P(R) und P(B):

 

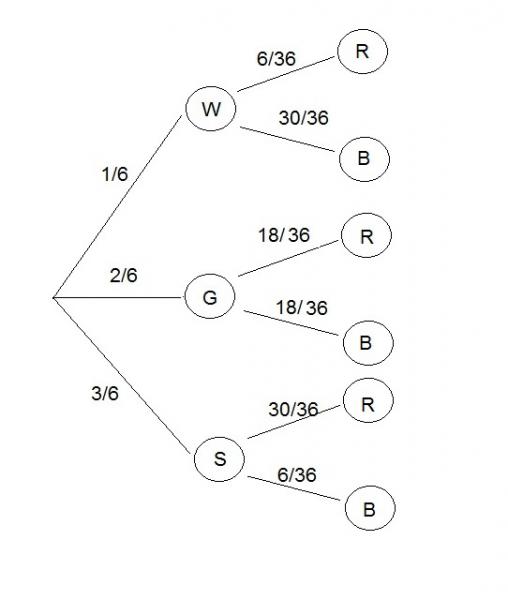
P(B) = 1/6*30/36 + 2/6*18/36 + 3/6*6/36 = 7/18

P(G) = 2/6

P(B) * P(G) = 7/18*2/6 = 7/54

G kommt zusammen mit  B nur in einem pfad vor: P(G∩B) = 2/6*18/36 = 1/6

P(G∩B) = 1/6 ≠ 7/54 =  P(B) * P(G) ⇒ P(B), P(G) abhängig

 

jetzt ein bildchen für den teil b), das inverse baumdiagramm für die bedingten wahrscheinlichkeiten:

 

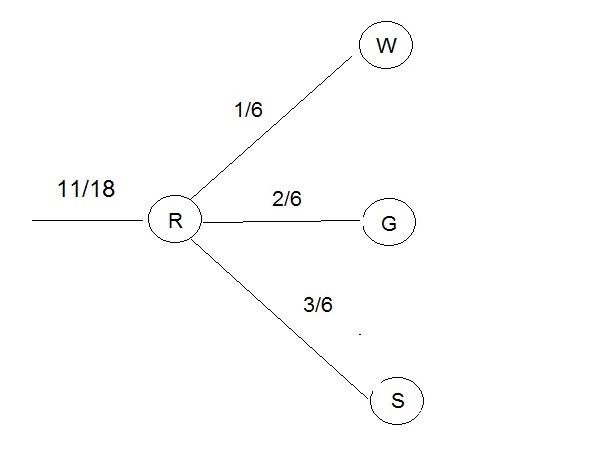
b)

 

P(R) = 1/6*6/36 + 2/6*18/36 + 3/6*30/36 = 11/18

P(W|R) = 1/6*11/18 = 11/108 ≈ 0,1019

P(G|R) = 2/6 * 11/18 = 11/54 ≈ 0,2037

P(S|R) = 3/6 * 11/18 = 11/36 ≈ 0,3056

 

c)

wie in a) kann man zeigen, dass G und R abhängig sind.

daher kann man an der schwarzen urne rumfummeln wie man lustig ist, man ändert zwar P(R) (und P(B)),

aber G und R bleiben abhängig.

 

lg

Comments

Danke für deine Hilfe, aber bei teil c) ich muss zeigen, wie sie unabhängig bleiben werden nicht abhängig.

---

durch die änderung der anzahl der roten und blauen steine in der schwaren urne kriegt man das nicht hin.

das habe ich in der antwort zu c) versucht zu erklären (wenn ich nichts wesentliches übersehen habe :D)

eine unabhängigkeit könntest du erreichen wenn du urne W und S entfernen würdest, oder wenn du alle roten kugeln aus allen urnen entfernen würdest. das ist gemäß aufgabe c) aber nicht vorgesehen.