Aufgabe:
Bestimmen Sie die Taylorreihe von
$$ k ( x ) = \frac { x } { ( 1 - x ) ^ { 2 } } $$
um \( x_0 = 0 \) durch gliedweise Differentiation einer geeigneten Potenzreihe. Geben Sie das größtmögliche offene Intervall \( ( a , b ) \subset \mathbb { R } \) an, auf dem die von Ihnen gefundene Reihe k tatsächlich darstellt.
Teil 1: habe ich soweit:
$$\frac{x}{(1-x)^2} = \frac{x}{x^2-2x+1} \leq \frac{x}{x^2-2x} = \frac{1}{x-2}= -1/2*\frac{1}{1-\frac{x}{2}}$$
Das ist die geometr. Reihe. und mit dem Wurzelkriterium komme ich auf: -4 < x < 4:
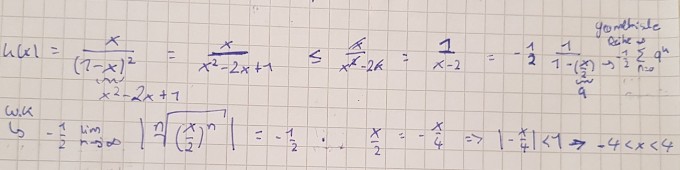
Ist das soweit einigermaßen okay?
Teil 2 sagt mir aber leider gar nichts.