Für das Volumen V eines Prismas gilt:
V = G * h
wobei G der Grundflächeninhalt und h die Höhe des Prismas ist.
Die Grundfläche ist vorliegend ein Deltoid, dessen Flächeninhalt G nach der Formel
G = e * f / 2
berechnet wird, wobei e und f die Längen der Diagonalen des Deltoids sind.
Während e bereits gegeben ist ( e = 8 ) , muss f noch berechnet werden. Dazu erstellt man sich zunächst eine Skizze, etwa so:
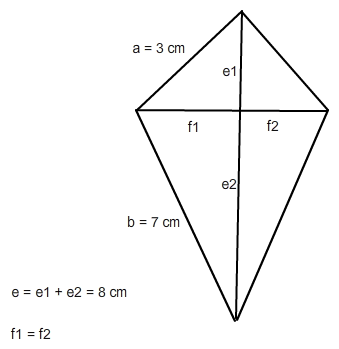
Wichtig ist zu wissen, dass die Symmetrieachse eines Deltoids die zweite Diagonale f halbiert, dass also gilt:
f1 = f2
Außerdem stehen in einem Deltoid beide Diagonalen senkrecht aufeinander.
Man hat also vier rechtwinklige Dreiecke, aus denen man unter Anwendung des Satzes von Pythagoras die Längen der Teile der Diagonalen berechnen kann.
Es gilt:
e1 ² + f1 ² = 3 ² = 9
e2 ² + f1 ² = 49
e1 + e1 = 8
Löst man dieses Gleichungssystem, so erhält man:
e1 = 1,5 cm
e2 = 6,5 cm
f1 = f2 = 2,5 cm also f = 5 cm
Somit beträgt der Flächeninhalt G des Deltoids:
G = e * f / 2 = 8 * 5 / 2 = 20 cm ² <--- Hier hatte ich vergessen, durch 2 zu dividieren.
und sein Volumen V
V = G * h = 20 * h
Auflösen nach der Höhe h ergibt:
h = V / 20
und mit V = 100 cm ³ ergibt sich:
h = 100 / 20 = 5 cm
Versuche nun selbst, den Oberflächeninhalt, also die Summe der Flächeninhalte aller das Prisma begrenzenden Flächen zu bestimmen.
Edit: Rechenfehler korrigiert.