Nullstellen bestimmen (Parabel 5. Ordnung)

Question

Guten Tag Miteinander

Wie bestimme ich die Nullstellen, dieser Funktion?

Aufgabe: y=x^5-5x+5

Mein Lösungsansatz: Ich versuchte zuerst eine Lösung zu erraten, habe jedoch keine Zahl gefunden, damit ich eine Polynomdivision durchführen konnte.

LG
Schindler

Answer 1

das ist ein Polynom 5ten Grades, da kann man die Nullstellen im Allgemeinen nicht raten oder analytisch bestimmen. Verwende ein Näherungsverfahren. Als Startwert bietet sich x=1.5 an.

Comments

Hier aber schon. Stichwort ist: Bring-Jerrard-Form!

---

Dann schreibe bitte die analytische Lösung in einem Kommentar hierher.

---

Siehe Wikipedia:

https://de.wikipedia.org/wiki/Gleichung_f%C3%BCnften_Grades#L%C3%B6sbare_Gleichungen_f%C3%BCnften_Grades

---

Dann ist die Aufgabe für den Fragesteller ja schon gelöst. ;)

---

Naja, er muss jetzt erst einmal gucken, dass er die \(-5\) in seinem Polynom irgendwie als \( \frac { 5 \mu ^ { 4 } ( 4 \nu + 3 ) } { \nu ^ { 2 } + 1 }\) mit \(\nu ,\mu ∈ℚ\) hinkriegt und \(5\) als \( \frac { 4 \mu ^ { 5 } ( 2 \nu + 1 ) ( 4 \nu + 3 ) } { \nu ^ { 2 } + 1 }\) auch mit \(\nu ,\mu ∈ℚ\) ausdrücken kann.

Answer 2

Bei dieser Aufgabe kommt man mit Raten nicht weiter.

Die bei Wikipedia vorgeschlagene "Spezialfall-Lösung" ist mir auch zu speziell: langes Suchen ohne Garantie auf Erfolg.

Was immer schnell und genau funktioniert ist (neben der langsameren Bisektion ) das Newton-Verfahren (schnell konvergierende Iteration).

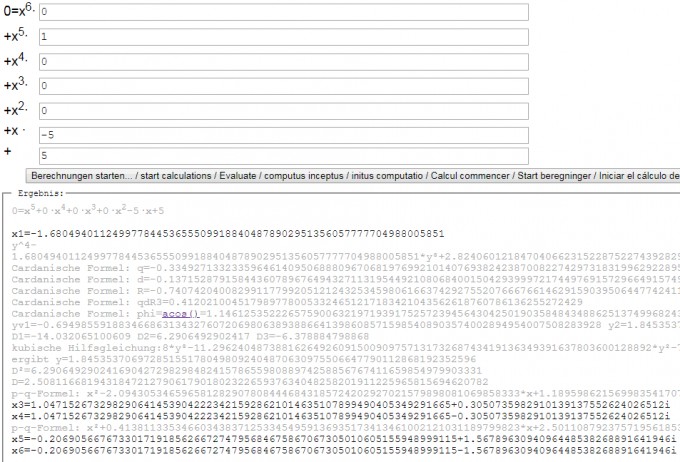
Nach der Division durch diese Nullstelle kann man die daraus gewonnene Gleichung 4. Grades entweder mit Cardanischen Formeln oder PQRSTUVW-Formeln explizit lösen: http://www.lamprechts.de/gerd/php/gleichung-6-grades.php

Ganz NEU für Interessierte:

Für Gleichungen der Form x^5-a*x+b=0

gibt es nun endlich auch einen expliziten Weg mit Hilfe der hypergeometrischen Funktionen:

x₁=-(-1)^{1/4} (-a)^{1/4} (((-1)^{3/4} *b*4F3(... )... wird zu lang hier

x₄=(b * ₄F₃(1/5, 2/5, 3/5, 4/5;1/2, 3/4, 5/4;(3125 b^4)/(256 a^5)))/a  {etwas kürzer}

=₄F₃[{1/5, 2/5, 3/5, 4/5},{1/2, 3/4, 5/4},625/256]=1.047152673298290641453904... -0.3050735982910139137552624... i

...

Zwar kann man diese Formeln "schön hinschreiben", aber die genaue Berechnung des Ergebnisses mit diesen Universal-Funktionen erfolgt über langsam konvergierende unendliche Reihen mit komplexen Zahlen -> was ein sehr großer Nachteil gegenüber der schnell konvergierenden Newton-Iteration ist. (das können nur extrem wenige Rechner genau berechnen)