Explizite und rekursive Formel

Question

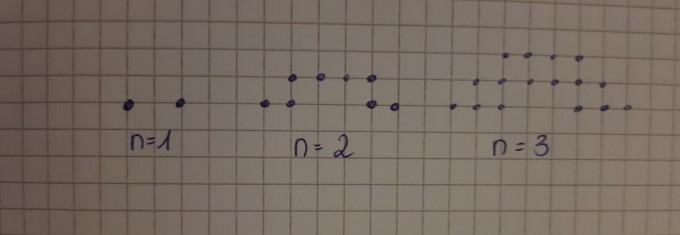
0. Bestimme die Anzahlen Bn für n = 1, 2, 3, 4, 5 sowie die Differenzen Bn+1–Bn für n = 1, 2, 3, 4
1. Stelle zwei explizite Formeln für die Folge der Bn auf, und zeige, dass sie gleichwertig sind.
2. Begründe, warum eine Ausdehnung der Folge nach B0 nicht sinnvoll ist.
3. Entwickle eine rekursive Formel für Bn (natürlich mit Startwert), und weise rech- nerisch nach, dass sie zur expliziten Formel in (c) gleichwertig ist.

Wir hatten das Heute gemacht und ich habe wirklich nicht vielverstanden, kann mir bitte jemand helfen und es mir erklären?

Comments

Bist du sicher, dass du korrekt abgezeichnet hast? Mir kommt das seltsam vor.

---

Ein paar mehr Bildchen braucht man schon, um ein Muster zu erkennen.

Answer 1

Nehmen wir an, es sei die Folge der Punktezahlen in den drei Bildchen gemeint. Dann beginnt die Folge mit 2, 8,16,...

Bilden wir uns jetzt ein, ein Muster erkannt zu haben und setzen die Folge fort:

2, 8,16, 26, 38, ...

In dieser Folge ist die zweite Differenzenfolge konstant. Sie besitzt also einen Funktionsterm der Form f(n)=an²+bn+c.die Punkte (1|2); (2|8);  (3|16) erfüllen diese Gleichung. Dann gilt f(n)=n²+3n-2. Damit hätten wir schon mal eine explizite Formel.

Mehr auf Nachfrage.

Comments

Kannst du mir bitte helfen, wie du auf 3n-2 gekommen bist?

---

Man setzt die Punkte (1|2); (2|8);  (3|16) in den Ansatz f(x)=ax²+bx+c ein und erhält so ein System von 3 Gleichungen mit 3 Unbekannten:

2=a+b+c

8=4a+2b+c

16=9a+3b+c.

Dieses hat die Lösungen a=1, b=3 und c=-2.

Also lautet die explizite Formel f(n)=n²+3n-2.