Steckbriefaufgaben Parabelgleichung mit Integration

Question

a) Eine quadratische Funktion mit einer Nullstelle bei x= 1, deren Hochpunkt auf der y- achse liegt, schließt mit den Koordinatenachsen im 1. Quadranten eine Fläche mit dem Inhalt 1 ein. Um  welche Funktion handelt es sich?

b) Eine quadratische Parabel schneidet die y-Achse bei -1 und nimmt ihr Minimum bei x= 4 an. Im 4 Quadranten liegt unterhalb der x- Achse über dem Intervall 0,1 ein Flächenstück zwischen der Parabel und der x- achse, dessen Inhalt 12 beträgt. Um welche Kurve handelt es sich?

c) Es handelt sich um eine nicht maßstäbliche Skizze einer Parabel. Bestimmen Sie deren Funktionsgleichung.

Comments

Das sind sogenannte Steckbriefaufgaben.

Ansatz: f(x) = ax^2 + bx + c.

Jetzt verwandelst du alle Angaben die du hast in Gleichungen und berechnest dann a, b und c (allenfalls noch D).

Du brauchst
z.B. f ' (x) = 2ax + b

und Stammfunktion von f

F = 1/3 ax^3 + 1/2 bx^2 + cx + D

Du kannst immer den gleichen Ansatz verwenden. Die Gleichungen bei b) und c) sollten sich aber von denen, die vorgerechnet wurden, unterscheiden.

Answer 1

Hallo Charlotte, 

a)

f(x) = ax² + bx + c

f'(x) = 2ax + b

f(1) = 0 = a + b + c

f'(0) = 0 = b

F(x) = 1/3 * a * x³ + 1/2 * b * x² + cx + d

F(1) - F(0) = 1 = 1/3 * a + 1/2 * b + c + d - d = 1/3 * a + 1/2 * b + c

3 Gleichungen, 3 Unbekannte

a = -1,5

b = 0

c = 1,5

Die Funktion lautet also

f(x) = -1,5x² + 1,5

 

Die anderen Aufgaben werden analog gerechnet :-)

Besten Gruß

Comments

Kannst du mir bitte erklären was du eingesetz hast und was wo?


das versteh ich nicht. =(

---

Hi Charlotte, 

eine quadratische Funktion hat die allgemeine Form

f(x) = ax² + bx + c

und die 1. Ableitung

f'(x) = 2ax + b

sowie die Stammfunktion

F(x) = 1/3 * a * x³ + 1/2 * b * x² + cx + d

wobei wir aber noch nicht wissen, welche Werte a, b und c haben. Deshalb müssen wir die gegebenen Informationen einsetzen:

 

1. Unsere gesuchte Funktion hat eine Nullstelle bei x = 1; also ist f(1) = 0; das setzen wir in die allgemeine Form ein: 

f(1) = a*1² + b*1 + c = 0; also: a + b + c = 0

 

2. Die gesuchte Funktion hat auf der y-Achse einen Hochpunkt; d.h. an der Stelle x = 0 (y-Achse) hat die Funktion den Anstieg 0 (notwendige Bedingung für einen Hochpunkt); Anstieg = 1. Ableitung; also:

f'(0) = 0 = 2a*0 + b; also b = 0

 

3. Die gesuchte Funktion schließt mit den Koordinatenachsen im 1. Quadranten (also x und y positiv)

eine Fläche mit dem Inhalt 1 ein.

Die Fläche hat also die linke Begrenzung x = 0 (die y-Achse) und die rechte Begrenzung x = 1, weil dort die Nullstelle ist. Also muss das Integral von 0 bis 1 den Flächeninhalt 1 haben. Dazu benötigen wir die Stammfunktion und rechnen F(rechte Grenze) - F(linke Grenze):

F(1) - F(0) = 1

F(1) = 1/3 * a * 1³ + 1/2 * b * 1² + c * 1 + d

F(0) = 1/3 * a * 0³ + 1/2 * b * 0² + c * 0 + d

F(1) - F(0) = 1/3 * a + 1/2 * b + c = 1

 

Jetzt hast Du für die 3 Unbekannten a, b und c die 3 Gleichungen:

a + b + c = 0

b = 0

1/3 * a + 1/2 * b + c = 1

 

Das kann man dann mit dem Einsetzungsverfahren oder mit dem Gauss-Algorithmus lösen - oder mit dem Taschenrechner :-)

 

Etwas klarer geworden?

 

Besten Gruß

---

hey, die 3 ist mir nicht klar geworden.  die 1 und 2 habe ich verstanden, aber die 3 verstehe ich nicht! =(

Kannst du sie mir vielleicht erklären?

---

Du meinst hier

"3. Die gesuchte Funktion schließt mit den Koordinatenachsen im 1. Quadranten..."

?

---

Genau das meine ich. Das verstehe ich leider nicht, kannst du mir das erklären? =)

---

Ich werde es versuchen :-)

Die Lösung haben wir ja schon, deshalb hier ein kleines Bild zur Veranschaulichung des 3. Teils:

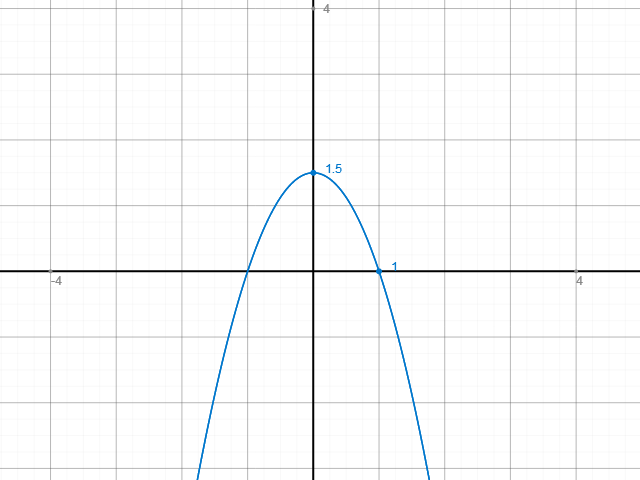
Es ist angegeben, dass die gesuchte Funktion mit den Koordinatenachsen im 1. Quadranten eine Fläche mit dem Inhalt 1 einschließt.

Das ist also die Fläche unter dem Bogen von (0|1,5) bis (1|0).

Wir wussten ja schon, dass die Funktion einen Hochpunkt auf der y-Achse hat, also die y-Achse schneidet, und dass die Nullstelle bei x = 1 liegt.

Und wenn uns dann noch gesagt wurde, dass die Funktion mit den Koordinatenachsen im 1. Quadranten eine Fläche einschließt, konnten wir uns schon ein ungefähres Bild von diesem Bogen machen.

Um eine Fläche unter dem Funktionsgraphen von f(x) zu berechnen, müssen wir die Stammfunktion bilden, und die Stammfunktion von f(x) = ax² + bx + c lautet 

F(x) = 1/3 * a * x³ + 1/2 * b * x² + cx + d

Ich hoffe, das ist Dir bekannt, ansonsten frag einfach nochmal nach.

Und schließlich:

Ein Integral zwischen zwei Grenzen berechnet man, indem man in die Stammfunktion den oberen Wert des Bereichs (hier 1) einsetzt und davon den Wert der Stammfunktion an der unteren Grenze (hier 0) subtrahiert:

F(1) - F(0)

Und das soll ja den Wert 1 ergeben ("... schließt ... eine Fläche mit dem Inhalt 1 ein.")

Also setzen wir ein:

F(1) = 1/3 * a * 1³ + 1/2 * b * 1² + c * 1 + d

F(0) = 1/3 * a * 0³ + 1/2 * b * 0² + c * 0 + d

Dann ist

F(1) - F(0) = 1/3 * a * 1 + 1/2 * b * 1 + c * 1 = 1/3 * a + 1/2 * b + c = 1

 

Etwas deutlicher geworden? 

Answer 2

Hier mal die Gleichungen für die Aufgabe b)

Eine quadratische Parabel schneidet die y-Achse bei -1

f(-1) = 0. Also: a*(-1)^2 + b*(-1) + c =0

und nimmt ihr Minimum bei x= 4 an.

f '(4) = 0 und a > 0.

2a*4 + b = 0  

 

Im 4 Quadranten liegt unterhalb der x- Achse (daher MINUS 12) über dem Intervall 0,1 ein Flächenstück zwischen der Parabel und der x- achse, dessen Inhalt 12 beträgt.

 1/3 ax³ + 1/2 bx² + cx + D  |₀¹  = -12

1/3 a*1^3 + 1/2 b*1^2 + c*1 + D - (1/3 a*0^3 + 1/2 b*0^2 + c*0 + D) = -12

1/3 a + 1/2 b + c  = -12

 

Um welche Kurve handelt es sich? 

Ansatz: f(x) = ax² + bx + c.

Jetzt verwandelst du alle Angaben die du hast in Gleichungen und berechnest dann a, b und c (allenfalls noch D).

Du brauchst
z.B. f ' (x) = 2ax + b

und Stammfunktion von f

F = 1/3 ax³ + 1/2 bx² + cx + D