Ich mache zunächst mal eine kleine Skizze:
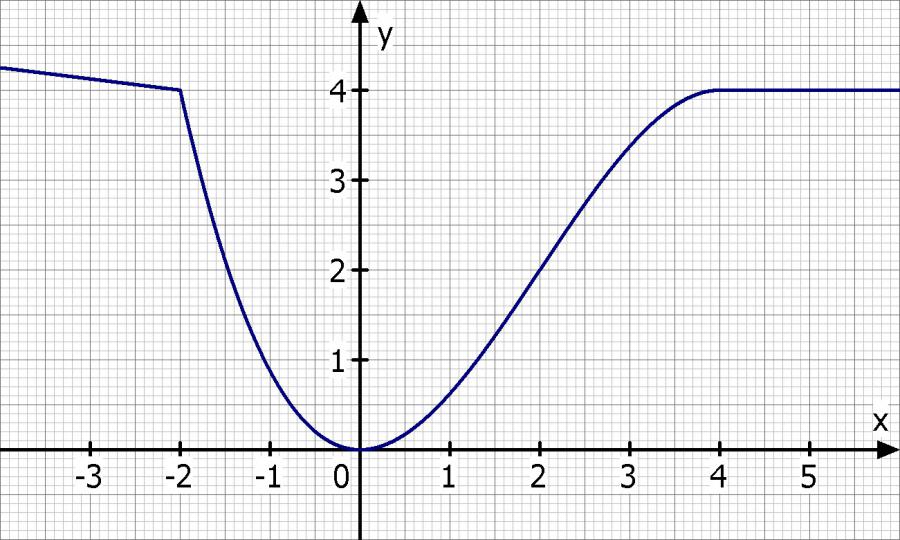
b) Von H soll eine unterirdische, gerade Leitung ausgehen und im Punkt B(u/f(u)) mit 0<u<4 ins Tal münden. Bestimmen Sie B so, dass die Leitung möglichst steil verläuft.
Damit die Leitung möglichst steil ist müssen wir durch H eine Tangente an f legen, die ihren Berührpunkt in B hat.
(f(u) - 4) / (u - 4) = f'(u)
(- u^3/8 + 3/4·u^2 - 4) / (u - 4) = 3/2·u - 3/8·u^2
- u^2/8 + u/4 + 1 = 3/2·u - 3/8·u^2
u^2/4 - 5·u/4 + 1 = 0
u^2 - 5·u + 4 = 0
u = 4 ∨ u = 1
f(1) = 5/8 = 0.625
Der Punkt ist (1, 0.625)
Skizze:
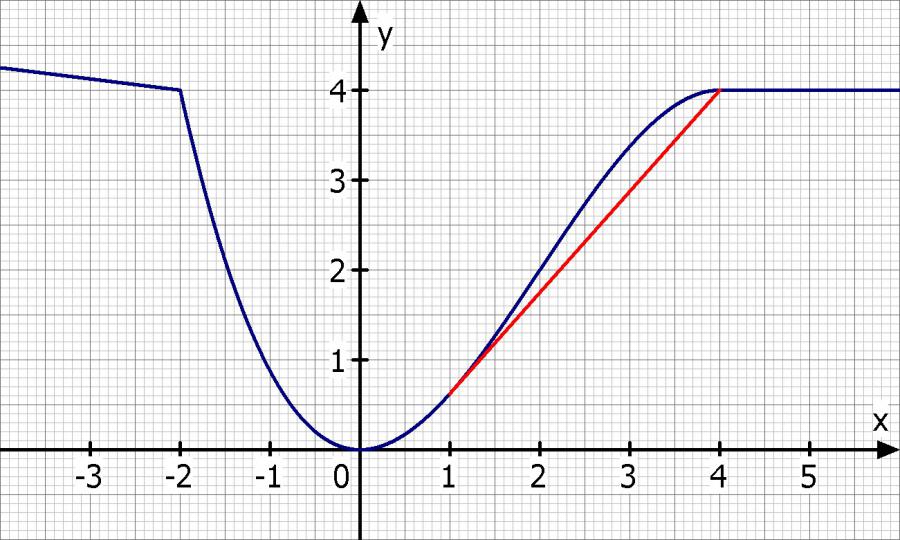
c) Bei Trockenheit ist der Wasserspiegel bis zum Punkt R(-1/f(-1)) abgesunken. Ab welcher Höhe über H ist dieser Punkt zu sehen?
Du legst jetzt nach dem obigen Schema eine Tangente von R an f und bestimmst dann den Funktionswert der Tangente an der Stelle 4.
Dann bestimmst du die Höhendifferenz zu H.