Hallo immai,
ich denke, es hilft ungemein, sich die komplexen Zahlen in der Gaußschen Zahlenebene vorzustellen. Jede komplexe Zahl lässt sich als Punkt oder Ortsvektor in einem kartesischen Koordinatensystem einzeichnen. Wobei der Realteil die X- und der Imaginärteil die Y-Koordinate ist. In Deinem Fall ist also $$\Re(z) = x= \sqrt2 , \quad \Im(z) = y= -\sqrt2$$ In der folgenden Skizze ist \(z\) als Ortsvektor dargestellt (der grüne Pfeil):
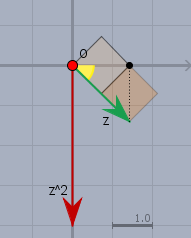
Jetzt sollte es kein Problem sein, \(z\) in das Koordinatensystem ein zu zeichnen. Es ist der grüne Pfeil, der vom Ursprung \(O\) zum Punkt \((\sqrt2|-\sqrt2)\) geht. Und dann fällt einen auch der (gelbe) Winkel \(\arg(z)\) in den Schoss: \(\arg(z)=-45°=-\pi/4\).
Wenn man nun weiß, dass \(\sqrt2\) die Länge der Diagonale eines Quadrats der Seitenlänge 1 ist, dann kann man sich vielleicht zwei kleine Quadrate vorstellen, deren Diagonalen parallel zu den Koordinatenachsen verlaufen und deren Seiten von dem Vektor \(z\) überdeckt werden. D.h. die Länge des Vektors ist \(|z|=2\).
Zwei komplexe Zahlen werden 'graphisch' multipliziert, indem ihre Winkel (Argumente) addiert und die Längen multipliziert werden. \(|z^2|\) ist das Quadrat von \(|z|\) und damit \(|z^2| = |z|^2 = 2^2 =4\). Und der Winkel von \(z^2\) ist nun auch kein Problem - er muss das doppelte von \(\arg(z)\) sein. \(\arg(z^2) = 2\arg(z) = -\pi/2\).
Gruß Werner