Gebrochenrationale Funktionen: Kanal mit Querschnitt (Rechtecks mit aufgesetztem Halbkreis) misst 8m^2

Question

Hallo

Aufg.

Es soll ein unterirdischer Kanal gebaut werden, dessen Querschnitt die Form eines Rechtecks mit aufgesetztem Halbkreis hat und 8m² misst. Wie müssen die Abmessungen dieses Querschnitts gewählt werden, damit sein Umfang minimal wird?

 

Lösung: Breite= Gesamthöhe= 8/√ (4+n)   m= 2.99 m

Ich verstehe nicht wie ich auf diese Resultat komme. Und warum in der Lösung 4 + n steht 

Bitte um Hilfe

Answer 1

Erst mal eine Skizze:

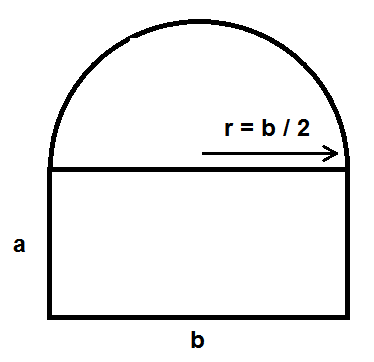
Für den Flächeninhalt dieser Figur soll gelten:

A = a * b + ( 1 / 2 ) * π * r ² 

= a * b  + ( π / 2 ) * ( b / 2 ) ²

= a * b +  π b ² / 8  = 8

<=> a = ( 8 - π b ² / 8 ) / b

<=> a = 8 / b - π b / 8

 

Für den Umfang U dieser Figur gilt:

U ( a, b ) = 2 a + b + π r

= 2 a + b + π b / 2

Für a den oben berechneten Term einsetzen:

U ( b ) = 16 / b - π b / 4 + b + π b / 2

<=> U ( b ) = 16 / b + π b / 4 + b

= 16 / b + ( ( 4 + π ) / 4 ) b

 

Der Umfang U soll minimal sein, also Extremwertbestimmung:

U ' ( b ) = 0

<=> - 16 / b ² + ( 4 + π ) / 4 = 0

<=>  ( 4 + π ) / 4 = 16 / b ²

<=> b ² = 64 / ( 4 + π )

<=> b = 8 / √ ( 4 + π )

(An dieser Stelle klärt sich nun so langsam, was es mit der von dir angegebenen Lösung auf sich hat ... das dort im Nenner stehende n ist kein n sondern ein π ! )

Rechnet man aus, so erhält man:

b = 2,99 m

(Auch das stimmt nun mit der von dir angegebenen Lösung überein!)

 

Nun muss noch der Wert von a berechnet werden. Einsetzen in die oben berechnete Bestimmungsgleichung für a ergibt:

a =  8 / b - π b / 8

= 8 / ( 8 / √ ( 4 + π ) ) - ( π / 8 ) * 8 / √ ( 4 + π )

= √ ( 4 + π ) - π / √ ( 4 + π )

[Multiplizieren des ersten Summanden mit √ ( 4 + π ) / √ ( 4 + π ) :]

= ( 4 + π - π ) / √ ( 4 + π )

= 4 / √ ( 4 + π )

Das ist gerade die Hälfte von b, also a = b / 2

 

Die Gesamthöhe h der Figur beträgt:

h = a + b / 2

= b / 2 + b / 2

= b

= 8 / √ ( 4 + π )

 

Rechnet man aus, so erhält man:

b = 2,993 m (gerundet)

a = 1,497 m (gerundet)

h = b = 2,993 m (gerundet)

A = a * b + π b ² / 8 = 8 m ²  (gerundet und wie gefordert)

U_min = 16 / b + ( ( 4 + π ) / 4 ) b = 10,69 m (gerundet)

Comments

U ( a, b ) = 2 a + b + 2 π b / 2 = 2 a + π b

Ich verstehe dies nicht, wäre hier nicht 2a + b+ πb ?

---

Verd... du hast recht . Das b ist mir entwischt. 

Was aber noch viel schlimmer ist: Ich habe die Berechnung mit einem Vollkreis angesetzt! Tatsächlich handelt es sich ja aber nur um einen Halbkreis. Damit muss ich die gesamte Berechnung neu machen ... :-(

Ich habe meine Antwort entsprechend bearbeitet - sie stimmt nun auch mit der von dir angegebenen Lösung überein (jedenfalls fast - Näheres dazu in der Antwort).

Toll übrigens, dass du meine Berechnungen nachverfolgt und diesen Fehler gefunden hast!