Vom Duplikat:
Titel: Hilfe geometrie zentrische streckung
Stichworte: geometrie,zentrische,streckung
Aufgabe 1: Zentrische Streckung
a) Zeigen Sie, dass je zwei Kreise mit verschiedenen Radien durch zentrische Streckungen aufeinander abgebildet werden können.
b) Gilt das auch für je zwei Quadrate oder zwei gleichseitige Dreiecke?
Aufgabe 2: Verketten zentrischer Streckungen
a) Was passiert, wenn man zwei zentrische Streckungen verkettet, also hintereinander ausführt? Geben Sie detailliert an, mit welcher Abbildung (EINE) man die Verkettung ersetzen kann. Unterscheiden Sie dabei die beiden Fälle, je nachdem ob das Streckzentrum gleich oder verschieden ist.
b) Wann lässt sich die Verkettung zweier zentrischer Streckungen als Verschiebung beschreiben?
Aufgabe 3: Verschiedene Arten von Konstruktionen
a)
Dritteln Sie eine DIN-A4-Seite! Vollziehen Sie dies auf vier verschiedene Weisen:
i. explorativ: Versuchen Sie möglichst genau durch Falten die Seite zu dritteln.
ii. euklidisch: Konstruieren Sie die Drittelung der Seite alleine mit Zirkel und Lineal.
iii. kartesisch: Nutzen Sie Maße oder Berechnungen, um die Seite zu dritteln.
iv. digital: Konstruieren Sie mit dem TI-Nspire eine Strecke mit beliebiger Länge.
Benutzen Sie die Tools des Rechners, um diese nur durch Konstruktionen (Punkt 7) zu dritteln. Überprüfen Sie anschließend die Richtigkeit Ihres Ergebnisses.
b) Vergleichen Sie die vier Konstruktionswege aus a) und beurteilen Sie diese hinsichtlich Effizienz, Gehalt für das Lernen von Mathematik, Tiefe des Verstehens, Genauigkeit, Eleganz und Spaß.
Aufgabe 4: Scherung nutzen
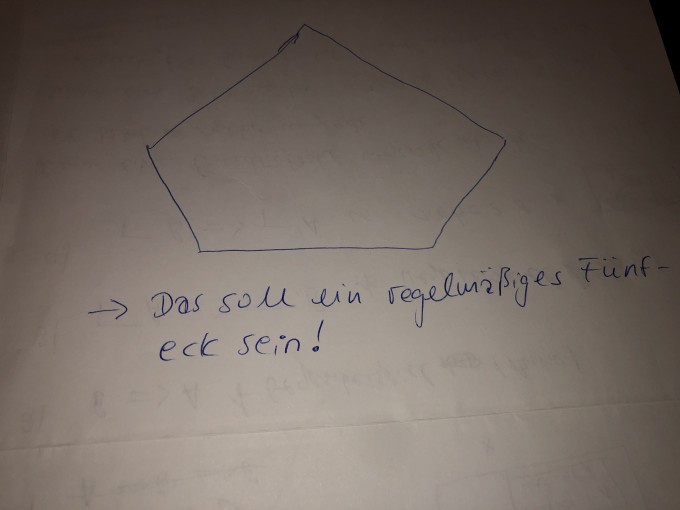
Verwandeln Sie per Konstruktion mit Zirkel und Lineal das folgende Fünfeck in ein flächeninhaltsgleiches Dreieck. Geben Sie eine Konstruktionsbeschreibung an.