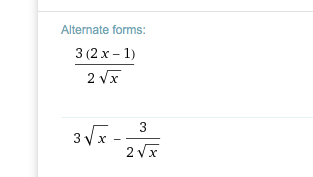Wurzeln im Nenner versucht man in Musterresultaten meist zu vermeiden.
D.h. hier noch vereinfachen:
f ' (x) = 2*√(x) + (2x - 3)/(2√(x))
= 2*√(x) + (2x)/(2√(x)) - 3 /(2√(x))
= 2*√(x) + √(x) - (3√(x)) / ( 2√(x) * √(x))
= 3 √(x) - (3√(x))/(2x)
Kann auch sein, dass bei euch zum Schluss ein einziger Bruchterm verlangt ist.
D.h. f ' (x) = ( 3√(x)(2x-1))/(2x)
https://www.wolframalpha.com/input/?i=2*√(x)+%2B+(2x+-+3)%2F(2√(x)) WA lässt die Wurzel aus x im Nenner stehen. Bsp: