Kettenregel mit einem Bruch

Question

Gegeben ist die Funktion

f(x)=             3

         ___________________________

                1+x^2

a) Für welche x  R ist f streng monoton abnehmend?

b) Untersuchen Sie die Funktion f  auf Extremstellen.

Wie muss ich vorgehen?

Comments

Würde ich nicht mit kettenregel ableiten sondern den Nenner mit einem negativen exponenten in den Zähler schreiben. Merke dir, verwende die Kettenregel nur, wenn es gar nicht anders geht. Sie ist unhandlich.

---

Ich weiss es wäre viel einfacher ohne Kettenregel allerdings muss ich diese anwenden, da ich sonst keine Punkte beim Test bekomme.

---

Dein Lehrer ist komisch .. du könntest den Bruch in $$3\cdot (1+x^2)^{-1}$$ umschreiben. Dann müsstest du aber die Produkt- und die Kettenregel anwenden. Oder du ziehst den konstanten Faktor 3 heraus und leitest nach der Reziprokenregel ab.

---

Sorry ich meinte eigentlich die quotientenregel die es zu vermeiden gilt. Kettenregel ist nicht so schlimm. Deswegen einen Bruch besser vor dem ableiten umwandeln.

Answer 1

Hallo Anna,

f(x)  = 3 / (1+x²)  =  3 · (1+x²)^-1

f '(x) = 3 · (-1) · (1+x²) ^-2 · 2x   = - 6x / (1+x²)²

Dann hast du - wie in meiner Antwort zu deiner letzten Frage - Potenz- und Kettenregel benutzt.  (# vgl. unten)

a)  f '(x)  ist für   x > 0  negativ und f ist dann streng monoton abnehmend

b)  f '(x) = 0  ⇔  x = 0

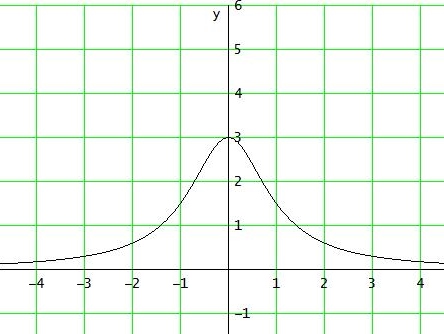
      Da f ' bei x=0  einen Vorzeichenwechsel von + → -  hat, liegt dort ein Hochpunkt

      f(0) = 3   →  H (0 | 3)  

Gruß Wolfgang

--------

(#) Nachtrag:

So geht die Ableitung wegen   [1/x] ' = -1/x²  auch:

[ 1 / u ] '  =_KR  -1 / u² · u '      mit u = 1+x²

[ 3 / (1+x² ] '  =  -3 / (1+x²) ²· 2x  =  -6x / (1+x²)²