Die exakt forumulierte Frage ist diese:
(b) Seien (xn), (yn) und (zn) reelle Zahlenfolgen, so dass (xn) beschränkt und (yn) eine gegen y=0 konvergente Folge ist, sowie (zn)
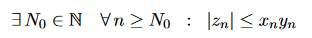
erfüllt. Beweise ausgehend von der Definition, dass (zn) ebenfalls gegen 0 konvergiert; gebe dazu das Nε an, so dass |zn−0|< ε für n > Nε.