Hallo Roland,
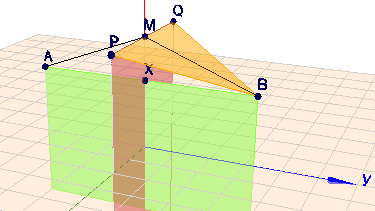
in der folgenden Zeichnung habe ich zwei der drei Rechtecke und eines der Dreiecke des Ikosaeders skizziert:
(klick auf das Bild zum Geoknecht3D)
Die Seitenlängen der Rechtecke betrage jeweils \(2a \times 2b\). Das Dreieck \(\triangle PBQ\) ist eine der Flächen des Ikosaeders. Die Strecke \(h=|MB|\) ist die Höhe in diesem Dreieck. Lt. Pythagoras gilt im rechtwinkligen Dreieck \(\triangle BMX\): $$h^2 = |MB|^2= |MX|^2 + |XB|^2 = (a-b)^2 + a^2 = 2a^2-2ab + b^2$$ Wenn der Körper ein Ikosaeder ist, so ist das Dreieck \(\triangle BMX\) ein gleichseitiges und die Höhe \(h\) im gleichseitigen Dreieck ist$$h = \frac 12 |PQ| \sqrt{3} = \frac 12 (2b) \sqrt 3 = b \sqrt 3$$ Einsetzen in vorherige Gleichung liefert: $$\begin{aligned} 2a^2 - 2ab + b^2 &= h^2 = 3b^2 \\ 2a^2 -2ab - 2b^2&= 0 \\ a^2 -ab - b^2&= 0 && \left| \div b^2\right.\\ \left( \frac ab \right)^2 - \left( \frac ab \right) - 1 &= 0 \end{aligned}$$ was bereits die bekannte quadratische Gleichung für das goldene Verhältnis \(\phi\) ist. Wie das Auflösen zeigt: $$\left( \frac ab \right) _{1,2} = \frac 12 \pm \sqrt{ \frac 14 + 1 } = \frac 12(1 \pm \sqrt 5)$$ ich hatte implizit angenommen, dass \(a \gt b\), dann bleibt: $$\frac ab = \frac12 (1+\sqrt 5) = \phi \quad \text{q.e.d}$$
Gruß Werner