Ein Rechteck R heißt goldenes Rechteck wenn es aus einem Quadrat und einem Rechteck S zusammengesetzt ist, sodass R und S ähnlich zueinander sind. Siehe unten:
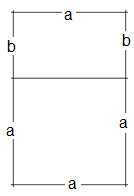
Wir drücken diesen Zusammenhang formal aus:
(a+b)/a=a/b
1+b/a=a/b und für a/b=x
1+1/x=x
x+1=x²
mit der positiven Lösung x=(√5 + 1)/2. a/b=(√5 + 1)/2 ist das größere Verhältnis des goldenen Schnittes und das Rechteck der obigen Abbildung heißt goldenes Rechteck.
Drei kongruente Rechtecke der Breite 2b und der Länge 2a werden so ineinandergeschoben, wie die Abbildung unten links zeigt. Benachbarte Ecken der Rechtecke werden miteinander verbunden, sodass das Kantenmodell eines Körpers mit 20 Seitenflächen (unten rechts) entsteht.

Wenn das Kantenmodell eines Ikosaeders entstehen soll, müssen alle Kanten gleichlang sein, insbesondere muss AB=AC sein. AB=\( \sqrt{a^2+(-b)^2+(b-a)^2} \) und AC=2b. Daraus folgt
a²+b²+b²-2ab+a²=4b² und nach etwas Umformung (insbesondere Division durch 2ab) folgt a/b-b/a-1=0. Nun setzen wir wieder a/b=x und erhalten die quadratische Gleichung x²-x-1=0 mit der positiven Lösung x=(√5+1)/2. Das bedeutet: Wenn die drei ineinander geschobenen Rechtecke kongruente, goldene Rechtecke sind, entsteht das Kantenmodell eines Ikosaeders (platonischer Körper mit 20 kongruenten gleichseitigen Dreiecken als Seitenflächen).