Kathetensatz/Satz des Thales usw | e Aufgabe

Question

Wie würde ich das lösen?

Danke für Eure Hilfe!!

Answer 1

Zeichne das "Netz" des Kartons oder nur zweier seine Wände. Zeichne den weg hinein.

Weg=√(30²+15²).

Comments

Welches Satz ist das? Das ist nur eine Wiederholung für mich.. ich habe das vor zwei Jahren gelernt :)

---

Das ist der Satz des Pythagoras a^2 + b^2 = c^2

@Roland: Müsste es nicht die Wurzel aus 35^2 + 10^2 sein?

Answer 2

es gibt insgesamt sechs Möglichkeiten für die Spinne um in 'gerader' Linie zur Fliege zu kommen. Wenn man den Quader in die Ebene aufklappt, kann man die sehen:

 

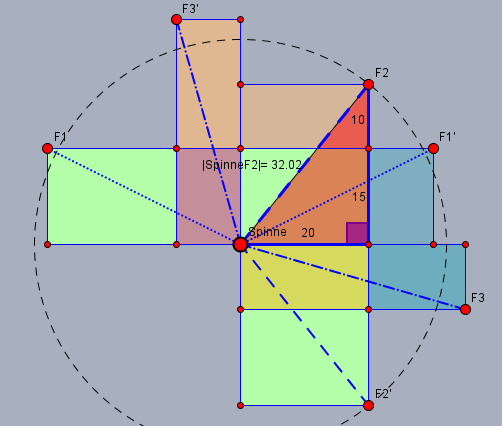
Davon sind jeweils zwei paarweise gleich lang. Das kürzeste Paar ist das mit der einfach gestrichelten Strecke von \(S_{\text{pinne}}\) nach \(F_2\) bzw. \(F_2'\). In dem rötlich markierten rechtwinkligen Dreieck mit den blauen Katheten gilt nach dem Satz des Pythagoras für die Strecke $$  |SF_2|^2 = 20^2 + (15+10)^2 \\|SF_2| = \sqrt{20^2 + 25^2} = \sqrt{1025} = 5\sqrt{41} \approx 32,02$$ Gruß Werner