Lagebeziehung zwischen 3 Ebenen- Sonderfall

Question

Aufgabe:

Ich habe 3 Ebenen in einem LGS(in Koordinatenform). Die Ebenen sind nicht parallel zueinander(da ihre Normalvektoren keine Vielfache voneinander sind. Sie sind aber linear abhängig voneinader.

Nun soll die Lage der drei Ebenen zueinander bestimmt werden.

Ich habe nun das LGS richtig gelöst, ich erhalte eine leere Menge mit Gauß(0=-2)

Die Lösung sagt das 3 Ebenen parallel zueinander sind.

Problem/Ansatz:

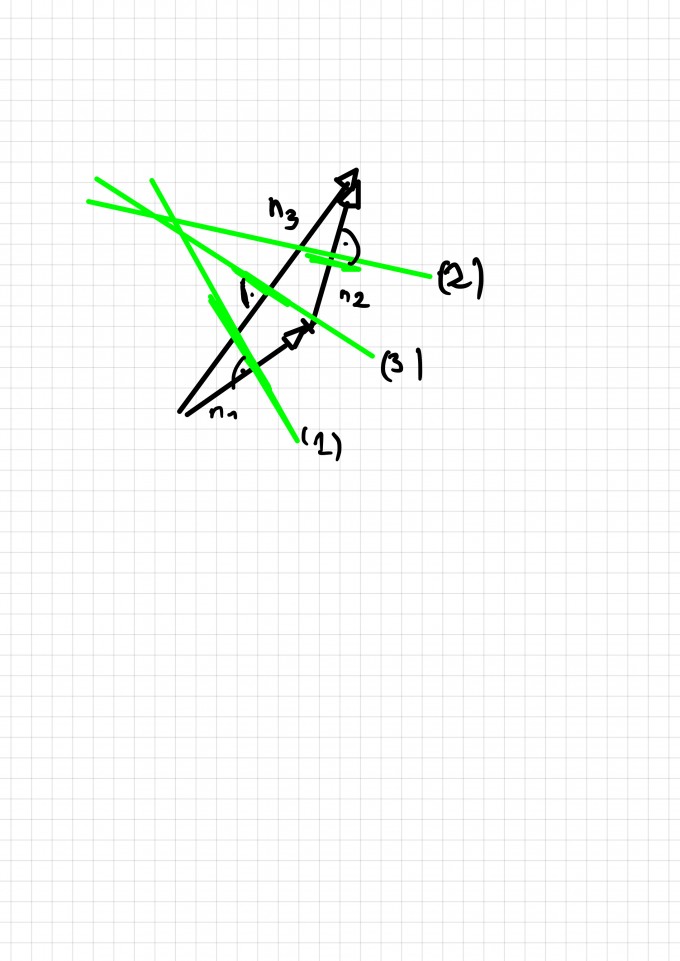
Da die einzelnen Normalenvektoren keine Vielfachen voneinander sind und es keine eindeutige/unendliche(von einer Variable abhängende) Lösung gibt war mein erster Lösungsansatz das die 3 Ebenen 3Schnittgeraden besitzen müssen. Immerhin kann ich doch eine Parallelität/Identität bei 3 nicht-parallenen Normalenvektoren ausschließen? Wenn ich drei lineare (Normalen)Vektoren auf ein Blatt Papier zeichne und dann die Ebenen(grün und in die Oberfläche hinein laufend) dazu nehme dann ist ein Schnittpunkt doch nicht ausgeschlossen? Wo ist mein Denkfehler, vielen Dank(siehe bild)

Answer 1

Ich habe nun das LGS richtig gelöst, ich erhalte eine leere Menge

Das heißt, es gibt keinen Punkt, der in allen drei Ebenen liegt. Das heißt nicht, dass die Ebenen parallel zueinander sind.

Stelle dir ein Prisma mit dreieckiger Grundfläche vor. Die drei Flächen des Mantels bestimmen die Ebenen. Die Normalenvektoren sind linear abhängig. Es gibt keinen Punkt, der zu allen drei Mantelteilen gehört.