Hallo Fataha,
Gesucht ist eine Zeit-Ort-Gleichung. Ein Ort \(\vec{p}\) ist eine Position in der Ebene mit zwei Koordinaten. Eine Zeit-Ort-Gleichung ist ein Gleichung, die einen Ort (bzw. Position) \(\vec{p}\) in Abhängigkeit der Zeit \(t\) liefert. Also $$\vec{p}(t) = ?$$
Da sich das Schiff geradlinig mit konstanter Geschwindigkeit bewegt, kann sein Ort als Geradengleichung in dieser Form angegeben werden: $$\vec{p}(t) = \vec{p}_0 + t \cdot \vec{v} $$ wobei \(\vec{p}_0\) die Position zum Zeitpunkt \(t=0\) ist (\(\vec{p}_0 = \vec{p}(t=0)\)) und \(\vec{v}\) gibt die Fahrtrichtung des Schiffes und in diesem Fall auch das Wegstück an, was das Schiff in einer Stunde zurücklegt - bzw. den Geschwindigkeitsvektor des Schiffs.
\(\vec{p}(t=0)\) ist gegeben: $$\vec{p}_0 = \vec{p}(t=0) = \begin{pmatrix} -2\\ -1 \end{pmatrix}$$ Den Vektor \(\vec{v}\) erhält man aus der Information, dass sich das Schiff nach einer halben Stunde bei \((-1|1)\) befinden muss. D.h. es muss gelten: $$\begin{aligned} \vec{p}(t=\frac 12) = \begin{pmatrix} -1\\ 1 \end{pmatrix} &= \vec{p}_0 + \frac 12 \cdot \vec{v} \\ \begin{pmatrix} -1\\ 1 \end{pmatrix} - \vec{p}_0 &= \frac 12 \cdot \vec{v} \\ \begin{pmatrix} -1\\ 1 \end{pmatrix} - \begin{pmatrix} -2\\ -1 \end{pmatrix} &= \frac 12 \cdot \vec{v} \\ \begin{pmatrix} 1\\ 2 \end{pmatrix} &= \frac 12 \cdot \vec{v} \\ 2 \begin{pmatrix} 1\\ 2 \end{pmatrix} &= \vec{v} \\ \begin{pmatrix} 2\\ 4 \end{pmatrix} &= \vec{v} \end{aligned}$$ Die vollständige Zeit-Ort-Gleichung lautet also $$\vec{p}(t) =\begin{pmatrix} -2\\ -1 \end{pmatrix} + t \cdot \begin{pmatrix} 2\\ 4 \end{pmatrix}$$
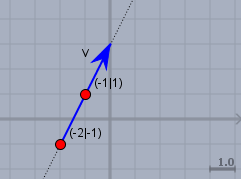
noch eine Skizze, um das Ergebnis zu veranschaulichen.