Elemente von Mengen durch Mengenoperationen bestimmen

Question

Aufgabe:

Gegeben sind die folgenden Mengen:

\( A=\{1,2,3,4,5,6,8,10,11,13\}, B=\{n \in \mathbb{N} | n \geq 6\} \)

\( \mathrm{C}=\{n \in \mathbb{N} | n \text { ist ungerade }\}, D=\{n \in \mathbb{N} | 2 n \leq 6\} \)

Bestimmen Sie die Elemente von \( A \cap B \). \( C \backslash B \) und \( D \backslash C \) und geben Sie diese, jeweils durch Kommata voneinander getrennt, an der dafür vorgesehenen Stelle ein. (Die Reihenfolge ist dabei unerheblich.)

Ansatz:

\( D \backslash C=\sqrt{0.2463} \) ist falsch.

Answer 1

wenn ℕ = {1, 2, 3, 4, 5, ...} ist (also ohne 0), dann gilt:


D = {n ∈ ℕ | 2n ≤ 6} = {1, 2, 3}

C = {n ∈ ℕ | n ist ungerade} = {1, 3, 5, 7, ...}


Somit ist D \ C

{2}

 

Ich liebe Venn-Diagramme :-)

 

Besten Gruß

Comments

Vielen Dank für die Hilfe :)

Darf ich Sie denn noch einmal beanspruchen?

Diesmal zu Ihren lieblings Thema Venn-Diagramme :)

 

Ich vermute hier das Antwort 2 richtig ist, aber bin nicht 100% sicher.

Sehen Sie das genauso?

---

Gern geschehen !!

Die Lösung dieser Aufgabe finde ich jetzt auf die Schnelle nicht - ich muss gleich weg.
Aber Sie bekommen die Antwort heute Abend, versprochen!

---

Dank noch mal für Ihre Mühe.

Aber bitte hetzen Sie sich blos nicht für mich :)

---

Kein Problem, habe mich nicht abgehetzt :-)

Es ist bei Aufgaben wie der Ihren hilfreich, die einzelnen Felder durchzunummerieren und dann die Klammern der einzelnen Ausdrücke von innen nach außen aufzulösen: 

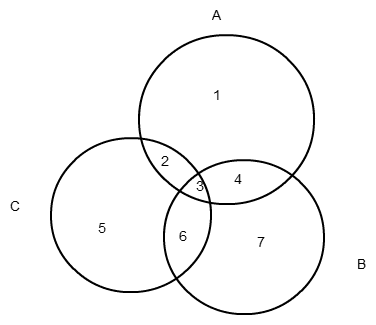
Fangen wir direkt mit Antwort 2 an: 

M = ((A∩(B∩C)) ∪ (A∩C∩B)) ∪ ((C∪B)\A) =

(A∩{3,6}) ∪ {3} ∪ ({2, 3, 4, 5, 6, 7}\A) =

{3} ∪ {3} ∪ {5, 6, 7} =

{3, 5, 6, 7}

 

Antwort 1: 

M = ((C∩B)\A) ∪ ((A∩(B∪C)) \ (A∩B∩C) =

{6} ∪ {2, 3, 4} \ {3} =

{2, 4, 6}

 

Antwort 3: 

M = ((C∪B) \ A) ∪ ((A∩(B∪C)) \ (A∩B∩C) =

{5, 6, 7} ∪ {2, 3, 4} \ 3 =

{2, 4, 5, 6, 7}

Antwort 3 ist also die richtige. 

 

Zur Kontrolle noch die Antwort 4: 

M = ((A∩(B∪C)) ∪ (A∩C∪B)) ∩ ((C∪B)\A) = 

({2, 3, 4} ∪ {2, 3, 4, 6, 7}) ∩ {5, 6, 7} =

{2, 3, 4, 6, 7} ∩ {5, 6, 7} = 

{6, 7}

 

Ich glaube, ich habe mich nicht verrechnet; aber selbst wenn, bin ich mir sicher, dass Sie die Vorgehensweise verstanden haben und jetzt selbst praktizieren können :-)

 

Besten Gruß

---

Das mit Nummer ist so simpel aber hilft mir wirlich um einiges.

Und Nummer 3 war auch richtig.

Ich probier gleich mal ein paar weitere Aufgaben.

Vielen lieben Dank und einen schönen Abend noch :)

---

Freut mich, wenn ich helfen konnte!

Viel Spaß beim Probieren :-)