Hallo Roland,
zur Berechnung der gewünschten Radien gibt es eine sehr schöne Möglichkeit, die ich Simon Pampena abgeschaut habe. O-Ton: "there's one way to solve this problem. It is absolute amazing".
Obiges Problem ist etwas einfacher, aber das Verfahren ist das gleiche. Zunächst zieht man um \(A\) eine Kreis (grün), mit dem Radius \(R=|AB|\). Anschließend invertiert man alle Kreise an diesem neuen Kreis. Man erhält dann zwei Geraden, für die Kreise \(K_1\) und \(K_2\) und drei gleichgroße Kreise für die kleineren.
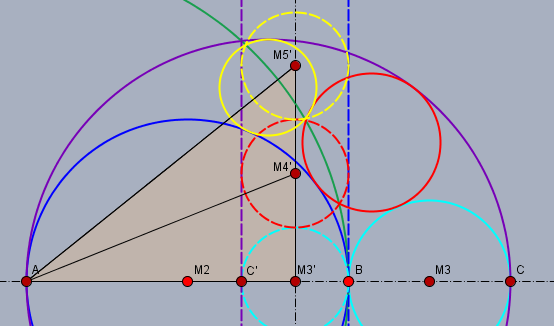
Wird ein Kreis mit dem Radius \(r\) an einem anderen mit dem Radius \(R\) invertiert und haben beide Mittelpunkte den Abstand \(x\), so ist der Radius \(r'\) des invertierten Kreises: $$r' = \frac{rR^2}{x^2-r^2}$$ Oben im Bild ist auf Grund der Inversion $$|AC'| \cdot |AC| = R^2 \implies |AC'| = \frac{R^2}{|AC|} = \frac{4^2}{6} = \frac 83$$ und weiter gilt $$|AM_3'| = \frac 12 \left( |AC'| + |AB| \right) = \frac 12 \left(\frac 83 + 4 \right) = \frac {10}3 \\ r'= |M_3'B| = |AB| - |AM_3'| = 4 - \frac{10}3 = \frac 23$$ damit liegt der Radius \(r'\) der drei invertierten Kreise bereits fest, Es muss nur noch der Abstand des jeweiligen Mittelpunkts von \(A\) berechnet werden. Für den roten Kreis mit Radius \(r_4\) gilt $$x_4'^2 = |AM_4'|^2 = |AM_3'|^2 + (2r')^2 = \frac{100}9 + \frac{16}9= \frac {116}{9} \\ \implies r_4 = \frac {r' R^2}{x_4'^2 - r'^2} = \frac{\frac 23 \cdot 4^2}{\frac {116}9 - \frac 49} = \frac 67$$ und für den gelben Kreis mit Radius \(r_5\) gilt $$x_5'^2 = |AM_5'|^2 = |AM_3'|^2 + (4r')^2 = \frac{100}9 + \frac{64}9= \frac {164}{9} \\ \implies r_5 = \frac {r' R^2}{x_5'^2 - r'^2} = \frac{\frac 23 \cdot 4^2}{\frac {164}9 - \frac 49} = \frac 35$$ Somit hat der erste Kreis im Schustermesser den Radius \(6/7\), der zweite den Radius \(3/5\) und der \(n\)'te hat den Radius $$r_n = \frac{6}{6+n^2}$$ Gruß Werner