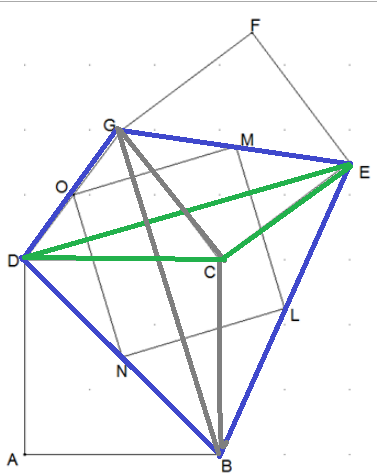
Ein bekannter Satz: Verbindet man in einem beliebigen Viereck (hier BEGD) die Seitenmittelpunkte miteinander, entsteht ein Parallelogramm (hier NLMO).
Das gilt, weil nach Umkehrung des Strahlensatzes NL und OM beide parallel zu DE sind (damit auch parallel zueinander) und weil LM und LO beide parallel zu BG (und damit auch zueinander) sind.
Die angesprochenen Seiten sind nicht nur parallel zu DE bzw. BG, sondern auch halb so lang wie diese.
Noch zu zeigen:
1) Das Parallelogramm NLMO ist sogar ein Rhombus. Dazu ist die Kongruenz der Diagonalen DE und GB nachzuweises, was wiederum mit einem erfolgreichen Nachweis der Kongruenz des grünen und des grauen Dreiecks möglich ist.
2) Der Rhombus NLMO ist sogar ein Quadrat. Dafür müssten DE und BG aufeinander senkrecht stehen, was sich wiederum unter Verwendung des grünen und des grauen Rechtecks bewerkstelligen lässt.