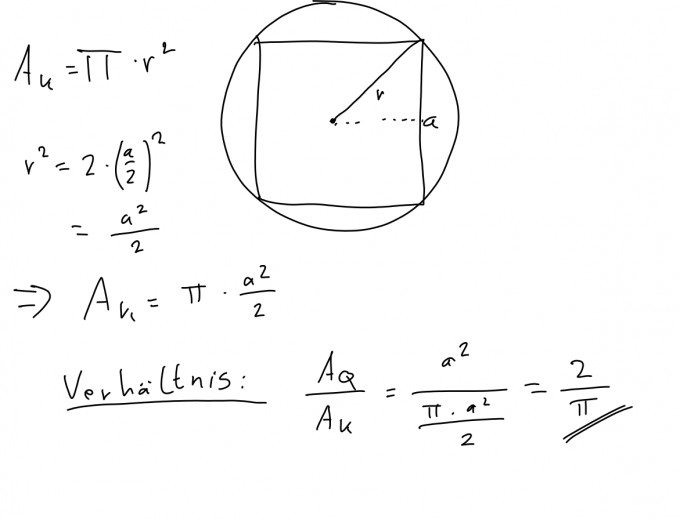Du rechnest mit dem Umfang des Kreises, was nicht gefragt ist. Die FLÄCHE.
$$ A_K=\pi \cdot r²\\A_Q=a^2 $$
Den Radius kann mit a so ausdrücken:
$$ r^2=2\cdot \Big(\frac{a}{2}\Big)^2 $$
Damit hat man
$$ A_K=\pi\cdot \frac{a^2}{2} $$
Und daraus ergibt sich das Verhältnis
$$ \frac{A_Q}{A_K}=\frac{a^2}{\pi\cdot \frac{a^2}{2}}=\frac{2}{\pi} $$