Sehr schöne Aufgabe!
Im gleichseitigen Dreieck schneiden sich auch die Seitenhalbierenden im Umkreismittelpunkt.
Seien A und B die beiden Punkte mit den kürzeren Loten zum Durchmesser. Dann ist die Länge des Lotes vom Mittelpunkt der Strecke AB auf den Durchmesser das arithmetische Mittel der Längen der von den Endpunkten A und B ausgehenden Lote.
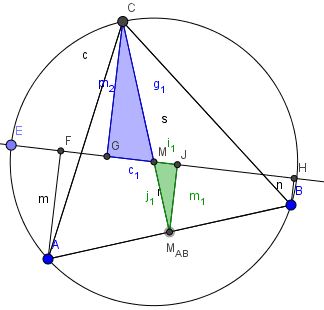
Das blaue und das grüne Dreieck (siehe Abbildung) sind ähnlich, zwischen entsprechenden Stücken beiden Dreiecke besteht das Längenverhältnis 2:1 (M teilt die von C ausgehende Seitenhalbierende in diesem Verhältnis.
Damit ist das längste Lot doppelt so groß wie das arithmetische Mittel der kürzeren Lote und damit genau so groß wie deren Summe.
(Der Sonderfall, dass der verwendete Durchmesser durch einen der Eckpunkte des Dreiecks verläuft, ist trivial.)