ich soll das Problem skizzieren - kann jemand helfen?
.. ich frage mich dann immer, wo genau Dein Problem liegt! Das wirst Du uns wahrscheinlich nicht verraten - oder?
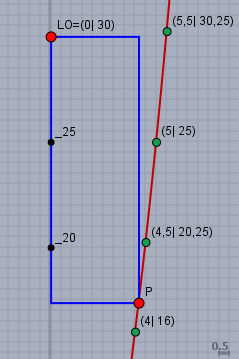
Nun - zeichne ein Koordinatensystem und da Dein DINA4-Blatt gerade 30cm hoch ist, solltest Du nicht bei \(y=0\) sondern vielleicht bei \(y=10\) am unteren Rand des Blattes anfangen. In das Koordinatensystem zeichnest Du den Punkt LO=\((0|\,30)\) (links oben) ein. Und dann berechnest Du einige Punkte der Parabel und zeichnest diese ebenso ein. Die verbindest Du dann zu einer Kurve. Diese Kurve ist der Graph der Parabel, auf dem Du nun einen beliebigen Punkt \(P\) wählst.
Ich unterstelle, dass die Seiten des Rechtecks parallel zu den Koordinatenachsen verlaufen sollen. Dann sieht das ganze aus, wie auf folgender Skizze:
(... und mit CindyJS funktioniert das nicht!)
und wahrscheinlich sollst Du nun die Position von \(P\) berechnen, bei der der Flächeninhalt des Rechtecks maximal wird.
Das was maximiert werden soll, ist allen Anschein nach die Fläche des Rechtecks. Die Breite des Rechtecks ist \(x\), wenn \(x\) die X-Koordinate von \(P\) ist. Die Y-Koordinate von \(P\) ist dann \(y=x^2\), da \(P\) auf der Parabel liegt. Die Höhe des Rechtecks ist dann folglich: \(h=30-y=30-x^2\). Folglich ist die Fläche \(F\) des Rechtecks: $$F=x \cdot (30-y)$$ für \(y\) nun das \(x^2\) einsetzen gibt: $$F= x\cdot (30-x^2)$$ Ableiten und Ableitung zu 0 setzen gibt \(x_{opt}=\sqrt{10}\).
Das kann man nach der Produktregel ableiten:$$F'(x) = (30-x^2) + x(-2x) = 30-x^2-2x^2=30-3x^2$$oder erst ausmultiplizieren$$F(x)=30x-x^3$$und dann ableiten:$$F'(x)=30-3x^2$$Setzt man die Ableitung zu 0, so gibt das$$\begin{aligned} 30-3x_{opt}^2&= 0\\ 30 &= 3x_{opt}^2 \\ 10&=x_{opt}^2 \\ \implies x_{opt}&= \sqrt{10}\end{aligned}$$
Bem. zum Definitionsbereich: aus der Anforderung 'Rechteck liegt im 1.Quadranten' folgt: \(x\ge0\). Weiter unterstelle ich, dass \(y \le 30\) gefordert ist, da man sonst aus einem unendlich großem \(x\) ein Rechteck mit unendlicher Fläche bilden kann.