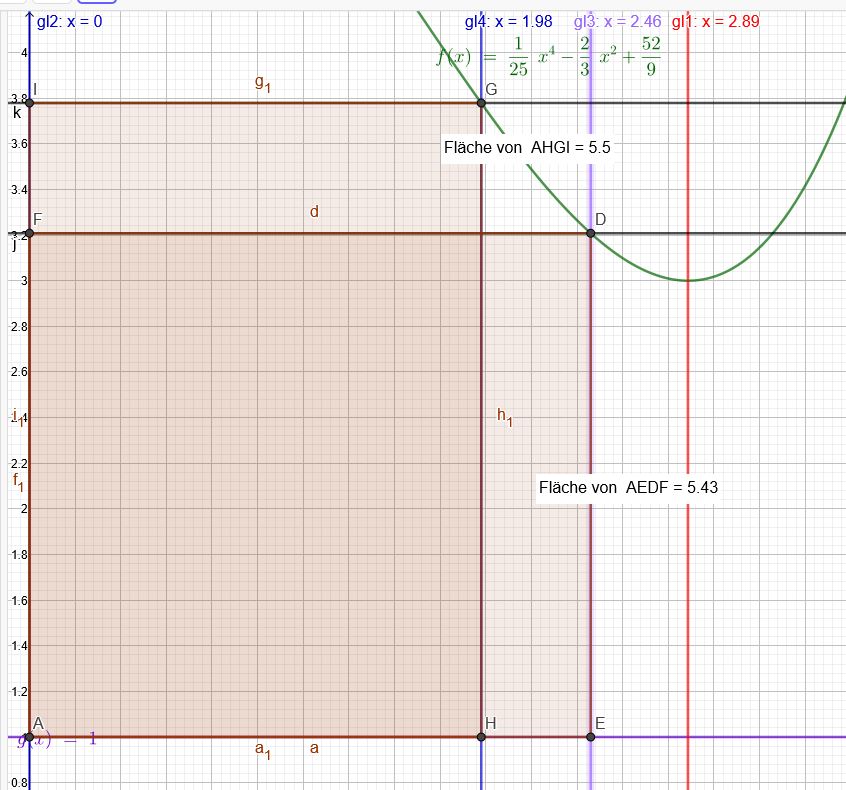
Zielfunktion:
\(A=u\cdot [f(u)-1]\) soll maximal werden.
Nebenbedingung:
\(f(u)= \frac{1}{25}u^4-\frac{2}{3}u^2 +\frac{52}{9}\)
\(A=u\cdot [\frac{1}{25}u^4-\frac{2}{3}u^2 +\frac{43}{9}]=\frac{1}{25}u^5-\frac{2}{3}u^3 +\frac{43}{9}u\)
\(A'=\frac{1}{5}u^4-2u^2 +\frac{43}{9}\)
\(\frac{1}{5}u^4-2u^2 +\frac{43}{9}=0\)
\(u^4-10u^2 =-\frac{215}{9}\)
\(u^4-10u^2+5^2 =-\frac{215}{9}+5^2\)
\((u^2-5)^2 =\frac{10}{9} |±\sqrt{~~}\)
1.)
\(u^2-5 =\frac{1}{3} \sqrt{10}\)
\(u^2 =5+\frac{1}{3} \sqrt{10}|±\sqrt{~~}\)
A)
\(u_1 =\sqrt{5+\frac{1}{3} \sqrt{10}}≈2,46\)
B)
\(u_2 =-\sqrt{5+\frac{1}{3} \sqrt{10}}≈-2,46\) Kommt nicht in Betracht.
2.)
\(u^2-5 =-\frac{1}{3} \sqrt{10}\)
\(u^2 =5-\frac{1}{3} \sqrt{10}|±\sqrt{~~}\)
C)
\(u_3 =\sqrt{5-\frac{1}{3} \sqrt{10}}≈1,98\)
D)
\(u_4 =-\sqrt{5-\frac{1}{3} \sqrt{10}}≈-1,98\) Kommt nicht in Betracht.
Flächenberechnungen führen zu dem maximalen u.